Lösung von Aufg. 11.1 S: Unterschied zwischen den Versionen
Wurzel (Diskussion | Beiträge) (→Aufgabe 11.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 11.1) |
||
| Zeile 2: | Zeile 2: | ||
Definieren Sie die Begriffe ''Innenwinkel eines Dreiecks'' und ''Außenwinkel eines Dreiecks''.<br /><br /> | Definieren Sie die Begriffe ''Innenwinkel eines Dreiecks'' und ''Außenwinkel eines Dreiecks''.<br /><br /> | ||
| − | Definitionsversuch 1 | + | ==Definitionsversuch 1, Tchu Tcha Tcha== |
(Innenwinkel eines Dreiecks):<br /> | (Innenwinkel eines Dreiecks):<br /> | ||
Es sei <math>\overline{ABC}</math> ein Dreieck. Die Winkel <math>\angle ABC , \angle BCA und \angle CAB</math> sind die Innenwinkel des Dreiecks <math>\overline{ABC}</math>.<br /> | Es sei <math>\overline{ABC}</math> ein Dreieck. Die Winkel <math>\angle ABC , \angle BCA und \angle CAB</math> sind die Innenwinkel des Dreiecks <math>\overline{ABC}</math>.<br /> | ||
| Zeile 8: | Zeile 8: | ||
(Außenwinkel eines Dreiecks):<br /> | (Außenwinkel eines Dreiecks):<br /> | ||
Ein Winkel, dessen Nebenwinkel ein Innenwinkel eines Dreiecks ist, nennt man Außenwinkel dieses Dreiecks.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:35, 5. Jul. 2012 (CEST)<br /> | Ein Winkel, dessen Nebenwinkel ein Innenwinkel eines Dreiecks ist, nennt man Außenwinkel dieses Dreiecks.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 12:35, 5. Jul. 2012 (CEST)<br /> | ||
| + | ==Definitionsversuch 2, Wurzel== | ||
| − | |||
ABC sei Dreieck.die Strahlen AC+ und AB+ bilden zusammen mit dem Scheitelpunkt S denn Innenwinkel Alpha. Bei innenenwinkel ist der Betrag < 180. Der nebenwinkel von Alpha heißt Außenwinkel Alpha '. Als gemeinsamen Schenkel hat der Außenwinkel den Strahl CA- oder AB-. | ABC sei Dreieck.die Strahlen AC+ und AB+ bilden zusammen mit dem Scheitelpunkt S denn Innenwinkel Alpha. Bei innenenwinkel ist der Betrag < 180. Der nebenwinkel von Alpha heißt Außenwinkel Alpha '. Als gemeinsamen Schenkel hat der Außenwinkel den Strahl CA- oder AB-. | ||
--[[Benutzer:Wurzel|H2O]] 13:47, 8. Jul. 2012 (CEST) | --[[Benutzer:Wurzel|H2O]] 13:47, 8. Jul. 2012 (CEST) | ||
| + | |||
| + | ===M.G.=== | ||
| + | Warum so kompliziert? Wenn Sie das Dreieck durch seine Eckpunkte bereits gekennzeichnet haben, dann können Sie doch die Innen in der Form <math>\angle Punkt_1, Scheitelpunkt, Punkt_2</math> kennzeichnen. Die Angabe zu den Größen hat in der Definition nichts verloren. Jeder zu jedem Innenwinkel gehören zwei Außenwinkel. Wenn Sie über den Begriff des Nebenwinkels Außenwinkel definiert haben, dann hat die Angabe der gemeinsamen Schenkel in der Definition nichts mehr verloren.--[[Benutzer:*m.g.*|*m.g.*]] 19:46, 8. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
Version vom 8. Juli 2012, 18:46 Uhr
Inhaltsverzeichnis |
Aufgabe 11.1
Definieren Sie die Begriffe Innenwinkel eines Dreiecks und Außenwinkel eines Dreiecks.
Definitionsversuch 1, Tchu Tcha Tcha
(Innenwinkel eines Dreiecks):
Es sei 
ein Dreieck. Die Winkel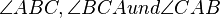 
sind die Innenwinkel des Dreiecks .
(Außenwinkel eines Dreiecks):
Ein Winkel, dessen Nebenwinkel ein Innenwinkel eines Dreiecks ist, nennt man Außenwinkel dieses Dreiecks.
--Tchu Tcha Tcha 12:35, 5. Jul. 2012 (CEST)
Definitionsversuch 2, Wurzel
ABC sei Dreieck.die Strahlen AC+ und AB+ bilden zusammen mit dem Scheitelpunkt S denn Innenwinkel Alpha. Bei innenenwinkel ist der Betrag < 180. Der nebenwinkel von Alpha heißt Außenwinkel Alpha '. Als gemeinsamen Schenkel hat der Außenwinkel den Strahl CA- oder AB-. --H2O 13:47, 8. Jul. 2012 (CEST)
M.G.
Warum so kompliziert? Wenn Sie das Dreieck durch seine Eckpunkte bereits gekennzeichnet haben, dann können Sie doch die Innen in der Form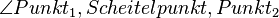 
kennzeichnen. Die Angabe zu den Größen hat in der Definition nichts verloren. Jeder zu jedem Innenwinkel gehören zwei Außenwinkel. Wenn Sie über den Begriff des Nebenwinkels Außenwinkel definiert haben, dann hat die Angabe der gemeinsamen Schenkel in der Definition nichts mehr verloren.--*m.g.* 19:46, 8. Jul. 2012 (CEST)
