Lösung von Aufgabe 11.4P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
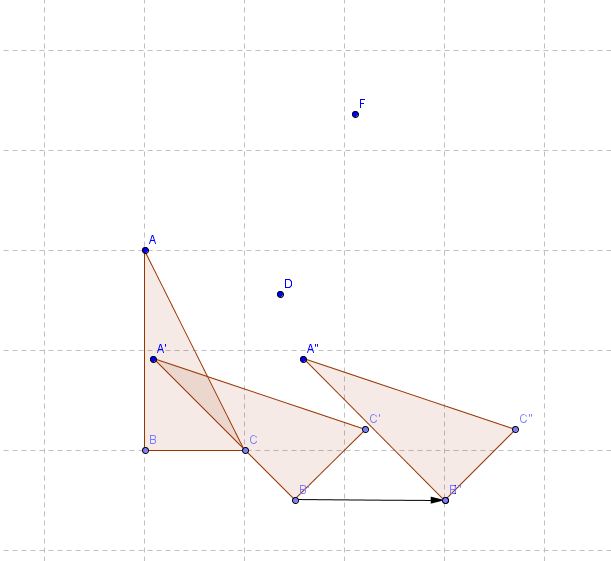
Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | ||
| − | <br /><br /> | + | <br /><br />[[Datei:11.4.JPG]]<br />--[[Benutzer:Studentin|Studentin]] 22:53, 1. Jul. 2012 (CEST)<br /> |
| + | hier noch die konstruktion von punkt p nachgeliefert :<br /> | ||
| + | <ggb_applet width="1281" height="493" version="4.0" ggbBase64="UEsDBBQACAgIACEI5EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIACEI5EAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VvbbuM2Gr6ePgWhi71YjGWeJFmzzhTjFMUOkHaCZlos9mZBS7SjRpa8kuzERR9qn2GfbH+SkizZimM7h3GyRlMd+JM/+X3/ibRn+P3dLEZLmeVRmpxZxMYWkkmQhlEyPbMWxaQ3sL7/+N1wKtOpHGcCTdJsJooziyvJKDyzBhMvwM540BOYhz3uD9yeP/Fpb0z8MfFYICj2LITu8uhDkv4sZjKfi0BeBddyJi7SQBRa8XVRzD/0+7e3t3alyk6zaX86Hdt3eWghmGaSn1nlzQcYrtXplmlxijHp/+OnCzN8L0ryQiSBtJBawiL6+N274W2UhOktuo3C4hoWTH2Y3bWMptewKJfBovpKag6IzGVQREuZQ9/Go150MZtbWkwkqv2duUNxvR4LhdEyCmV2ZmGbeJj5jBKHEOL5LncslGaRTIpSmJRK+9Vww2Ukb8246k6r5BYq0jQeCzUk+vNPRDHF6L26EHOhcHFd04TNO8zMhZoLNxfHyHDTnRtRbmS4keHMQssoj8axPLMmIs4BwyiZZMBf/ZwXq1jq+ZQv1ssn72FNefQHCDMMmBrQ4T3G79WfC38cl2A3FkkaWotscaDSSiWhA7K/TvqolbJKKaUdOqlzzzrdHUrNwvdaqNPAFlTp//Tflka2a5mbGs3z4xS6/EWWOOxXvjIs3QPl10q2NJ9CznLlMMxHjq/sniAHnMP1wMwdRHy4eBSBOyDiIO7AIxkgV109xDxo4IihAVJyhCHtHc4A/sc9PZiLHBhMvfXAKREBRRw5DBHtVByBKyHtmOCklIGE4yAHOin1hKohmIu4C09sgDjMUfmkR0CQQUd4BvUUMYKY6kw8RF3kqvEIV77uDtTUYUiKXIxcogYEtwaXNu4M8gPE1GrcEq4omS+KFkTBLKxui3RecwHSEJDWcc8EqFZYfDeMxVjGkCquFJMILUWsPEIrmqRJgWqHNO+mmZhfR0F+JYsCeuXod7EUF6KQdz+CdF7p1rJBmuSXWVqcp/FiluQIBWmM6zmnMWnc03rW8MAaDbzZ4DQa3Ma916k3hRa0yCXoT7O8Ehdh+FlJrEMDIPkliVejTIqbeRq1lzHs66wzlIsgjsJIJL+BsSotChe0TkIqXlVJiPu0mkmahVerHEwY3f1TZilgy12bNT8WWpkW6vs2aXzA3fNAxDow2bTxIb7q1N1GCTeq5bKmSNzJ9WqnmXLtxsPnfJTG61cagHMxLxaZLiBAVaZW9SmZxlIbiXZtyM7BzTi9uzLWwcxYX1dzeMJmBuOpBh5BcKAOJMxpeR2bq5ZRU6ulsJbBWgJX5haFdTsBWJWEvo7NVUuB/ZqplUsl1TIJrtREuQ5p2CodpwpXyvpVrl8kUXFRPRRRcLNequrw82I2lrUNtcckTzXmsL9hZMMbmSUyLm0ayFyki9y4aMPcQxlEM3g0DSUkQtH1K0zAvA3lNJPVxGNdnBnAdCtuWuvWaz3Uj1k6+5wsv4ItbExg2K9mOcyDLJorm0NjyAM3cm1VYZQLSCNhs59yQlh6oNIFwFMoaMA9F8V1munyC6IKXJXvxXIGtRYqtHlpC61h/qSrOIUnSse/Q2Crc59pXxMGzZ2mpo1SxPNroSq9ctGxWMmsBYMe76c03AQHsNcrACefG27nUhqzMPOFmzkMp72pFaUA7RzdnVk9ZmNItSvIjjZY9h+miDdFrFqr8rFWYDZvN4gC6zEwPQDY6A0ARivAmK3qsGdG7Pz1I8Zs19WAcdt9GhML0tlMJCFKdDV4mcaraZpY6/pEYOWbSBBlcUhQBaPBaFFU7RDlYkgjxIgFRkzABQqAsVFYqulgyCisOKiHaueDAmqVG9iR5XqTUJTpSd/8PQpDqevU/m56G4A2+SUO0ww7pExYa4LJIQTfb4W5nKqneiLBA3Z4+EQPtMS1PdUOqI8bjDlh4vjrz2AzNe9Phfx3YrrkJl9Gs3kcBVFR20+sLP1zUkD2lDp9bCfFGynnqhr5knzNRJKrMw8j00i2e8IuTgf2HrG5W2YKT+Peo9j2fczfDNrjE0Ib284ANz9EY99zS/AZJG7Pfb2W3k5zV0eluaq0N4mOYPptE532C53nON+Z55yj8twvaQFVaXea8/Ff//sfk8OutlLdp7+IeZr/7aGk1qpsyy7ftPhYI8ttn/nNj2OcgdvsGQqKTqBHewA9Ohzo0WkB7dqQPDW07OWgPd8D2vPDoT0/LWgd26GtgG5smNq89RbvDh1PWiKXAJlCuX6gLbQ7i+Zmx6DZUdQPqozej7PuYrpB3lstqfeyz2ee7kaFh0ubxC2jJMYkme2RpgmzV1t8bJXZJ0dFVUuUVbcq+CAJvuJ6b6vWPjXI3QrxzcrbWH+PQQDfPvR9Nfi3c+MP27i3T5Bf+FxJ8XZ4wU2wzWl5Fuc9R978DZBJs81ypZn9ftjKkYvd+W5phqxwXhznAE+482lW2QO/o8omNmsX375Geq3oCGdoHPeX7hCIrJB5JJIyfxfwfKnYQvJuvlH/3UeXdoq4Y5PUZGxx3/7o6F3SadWZvj0wx2M9CgnjGZziPpRHu1EeHYvy6BRRJsQeeBtOYdL1i2J+vhvz82MxPz9JzJ873O/cJnVsljq2THttnDq2Tx2bqI6t1OM3VP8326pTKy+bmyu2nU2JA/Fk8HaO0sWJstDcVznbNLhQAzn87dAwPk0a7t1rVZst17Ndzl/TbredSa5KHjoPOneninB3eN9kODyOVdz6TZTi9vH5GW+WRKYmArLdcgvNwele0xZ6H1JHXSXBJqnyMFLlU5D6ZOfWxBRdhNk+abI7KFlltsPpa4qZ+9BafrG2tTds0To5jNbJcbQq71wH4CeidaB/vaRopds7GUUrpyABm5nXSusFTHkU5V0nOOEWkbOoKCRoTW4yGVwX8l9kN7MKj5q2js7H75iOCMlfJpNcFrq88UxepXQ/I+iZ2Lzqjt1gBVz5/DNF7KOokw9S9wjinoC2Q7yzwRstv9D29t1MdMTiVRWrVR3r2Jzwxj7jhCicPOx99DHeR4+i8fggu6aRljs8vi+LHaF3VYVm85WP61Dv27FYB+cNCjsins6WXb7YYvrykEOoyxf+UdCayPKreWfPcynYrVCXe+6g/mJUJ1bXt7HD3PJAkFKbucTtPK7a9wdB/ebv1vW/Dyn/tePH/wFQSwcIVNU+RUoJAACKOQAAUEsBAhQAFAAICAgAIQjkQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAhCORAVNU+RUoJAACKOQAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAOEJAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />--[[Benutzer:Studentin|Studentin]] 01:02, 4. Jul. 2012 (CEST)<br /> | ||
| + | sehr gut!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 20:16, 5. Jul. 2012 (CEST) | ||
| + | |||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 9. Juli 2012, 21:39 Uhr
Zeigen Sie, dass die Verkettung einer Drehung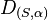 
mit einer Verschiebung wieder eine Drehung 
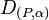ergibt. Wo liegt das neue Drehzentrum P?
--Studentin 22:53, 1. Jul. 2012 (CEST)
hier noch die konstruktion von punkt p nachgeliefert :
sehr gut!--Tutorin Anne 20:16, 5. Jul. 2012 (CEST)
