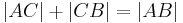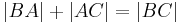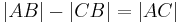Lösung von Aufgabe 6.9: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 95: | Zeile 95: | ||
...und jetzt? | ...und jetzt? | ||
--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] | --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] | ||
| + | |||
| + | Ich glaube, es ist noch zu zeigen, dass genau einer zwischen den beiden anderen liegt. Habe deinen Beweis ab Schritt IV weitergeführt: | ||
| + | |||
| + | {| class="wikitable " | ||
| + | |+ Beweis | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IV) | ||
| + | | <math>\operatorname{zw}\left \{A, B, C \right \}</math> oder <math>\operatorname{zw}\left \{A, C, B \right \}</math> oder <math>\operatorname{zw}\left \{B, A, C \right \}</math> | ||
| + | | Def (Zwischenrelation) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(V) | ||
| + | | zu zeigen: es liegt genau einer zwischen den beiden anderen | ||
| + | <br /> Annahme: es gilt <math>\operatorname{zw}\left \{A, B, C \right \}</math> und <math>\operatorname{zw}\left \{A, C, B \right \}</math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VI) | ||
| + | | <math>\left| AB \right| + \left| BC \right| = \left| AC \right| </math> | ||
| + | <br /><math>\left| AC \right| + \left| CB \right| = \left| AB \right| </math> | ||
| + | | (Axiom II/3) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VII) | ||
| + | | <math>\left| AB \right| + \left| BC \right| = \left| AC \right| </math> | ||
| + | <br /><math>\left| AB \right| - \left| CB \right| = \left| AC \right| </math> | ||
| + | | rechnen mit reellen Zahlen, (Axiom II/2) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VIII) | ||
| + | | <math>\left| AB \right| + \left| BC \right| = \left| AB \right|- \left| BC \right| </math> | ||
| + | | (VII gleichgesetzt), rechnen mit reellen Zahlen | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IX) | ||
| + | | <math>\left| AB \right| + 2 \left| BC \right| = \left| AB \right| </math> | ||
| + | | (VIII), + <math>\left| BC \right|</math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(X) | ||
| + | | <math>\ 2 \left| BC \right| = 0 </math> | ||
| + | | (IX), - <math>\left| AB \right|</math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(XI) | ||
| + | | Widerspruch, da das zweifache eines Abstands nicht null ergeben kann. | ||
| + | <br />--> Annahme zu verwerfen, Behauptung wahr. | ||
| + | | | ||
| + | |} | ||
| + | --[[Benutzer:Löwenzahn|Löwenzahn]] 17:58, 4. Jun. 2010 (UTC) | ||
Version vom 4. Juni 2010, 18:58 Uhr
Vorlage
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  ..., dann ... .
..., dann ... .
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
...
Behauptung
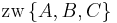 oder
oder 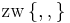 oder
oder 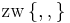
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 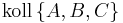
|
Voraussetzung |
| (II) | Element | Element |
| (III) | Element | Element |
| (IV) | Element | Element |
| (V) | Element | Element |
Versuch I
Satz:
- Von drei paarweise verschiedenen Punkten
 und
und  ein und derselben Geraden
ein und derselben Geraden  liegt genau einer zwischen den beiden anderen.
liegt genau einer zwischen den beiden anderen.
- Von drei paarweise verschiedenen Punkten
Beweisen Sie diesen Satz.
Satz in wenn-dann:
- Wenn drei Punkte
 und
und  kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten (und umgekehrt???) .
kollinear sind, dann liegt genau einer zwischen den beiden anderen Punkten (und umgekehrt???) .
- Wenn drei Punkte
Beweis
Es seien also  und
und  drei Punkte.
drei Punkte.
Voraussetzungen:
koll( und
und  )
)
Behauptung
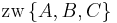 oder
oder 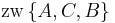 oder
oder 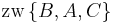
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 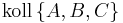
|
Voraussetzung |
| (II) | Für drei beliebige Punkte  und und  gilt: gilt: 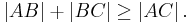
|
Axiom II/3: (Dreiecksungleichung) |
| (III) | 
|
Axiom II/3.1
|
| (IV) | ||
| (V) |
...und jetzt? --Heinzvaneugen
Ich glaube, es ist noch zu zeigen, dass genau einer zwischen den beiden anderen liegt. Habe deinen Beweis ab Schritt IV weitergeführt:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (IV) | 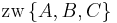 oder oder 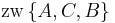 oder oder 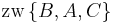
|
Def (Zwischenrelation) |
| (V) | zu zeigen: es liegt genau einer zwischen den beiden anderen
| |
| (VI) | 
|
(Axiom II/3) |
| (VII) | 
|
rechnen mit reellen Zahlen, (Axiom II/2) |
| (VIII) | 
|
(VII gleichgesetzt), rechnen mit reellen Zahlen |
| (IX) | 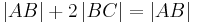
|
(VIII), + 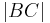
|
| (X) | 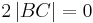
|
(IX), - 
|
| (XI) | Widerspruch, da das zweifache eines Abstands nicht null ergeben kann.
|
--Löwenzahn 17:58, 4. Jun. 2010 (UTC)