Lösung von Zusatzaufgabe 10.1 S: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:<br /> a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.<br /> Wenn in einem Dr…“) |
(→Anmerkungen Buchner zu den Beweisen "Umkehrung Basiswinkelsatz" von Tchu Tcha Tcha und RitterSport) |
||
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:<br /> | Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:<br /> | ||
a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.<br /> | a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.<br /> | ||
| − | Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] | + | Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.<br /> |
| + | |||
| + | b) '''BEWEIS BASISWINKELSATZ'''<br /> | ||
| + | <br /> [[Datei:Zusatz 10.1b.png]]<br /> | ||
| + | |||
| + | Vor. <math>a \tilde {=} b</math> <br /> | ||
| + | Beh.: <math>\alpha \tilde {=} \beta</math> <br /> | ||
| + | |||
| + | (1) <math>a \tilde {=} b</math> // Vor. <br /> | ||
| + | (2) es existiert w (die WH von <math>\gamma</math>) // Ex. & Eind. der WH<br /> | ||
| + | (3) <math>\ w \cap \overline{AB} = \{S}</math> // Vor., (1), Lemma 1<br /> | ||
| + | (4) <math>\left| \angle ACS \right| \tilde {=} \left| \angle DCS \right| \tilde</math> // (2),(3), Def. WH<br /> | ||
| + | (5) <math>\overline{CS} \tilde {=} \overline{CS}</math> // trivial, Vor., (3)<br /> | ||
| + | (6) <math>\overline{ACS} = \overline{ACS}</math> // (1),(4),(5), SWS<br /> | ||
| + | (7) <math>\angle SAC \tilde {=} \angle SBC</math> // (6), Dreieckskongruenz<br /> | ||
| + | (8) Beh. stimmt // (7)<br /> | ||
| + | qed<br /> | ||
| + | |||
| + | d) '''BEWEIS UMKEHRUNG BASISWINKELSATZ'''<br /> | ||
| + | <br /> [[Datei:Zusatz 10.1d.png]]<br /> | ||
| + | |||
| + | Vor.: <math>\alpha \tilde {=} \beta</math> <br /> | ||
| + | Beh.: <math>a \tilde {=} b</math> <br /> | ||
| + | |||
| + | (1) <math>\alpha \tilde {=} \beta</math> // Vor. <br /> | ||
| + | (2) es existiert w (die WH von <math>\gamma</math>) // Ex. & Eind. der WH<br /> | ||
| + | (3) <math>\ w \cap \overline{AB} = \{S}</math> // Vor., (1), Lemma 1<br /> | ||
| + | (4) <math>\left| \angle ACS \right| \tilde {=} \left| \angle BCS \right| \tilde</math> // (2),(3), Def. WH<br /> | ||
| + | (5) <math>\angle ASC \tilde {=} \angle BSC</math> // nach Vor., (4) und Innenwinkelsumme im Dreieck<br /> | ||
| + | (6) <math>\overline{CS} \tilde {=} \overline{CS}</math> // trivial, (3)<br /> | ||
| + | (7) <math>\overline{ASC} \tilde {=} \overline{BSC}</math> // (4),(5),(6),WSW<br /> | ||
| + | (8) <math>a \tilde {=} b</math> // (7), Dreieckskongruenz <br /> | ||
| + | (9) Beh. stimmt // (8)<br /> | ||
| + | qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:53, 30. Jun. 2012 (CEST)<br/> | ||
| + | <br/> | ||
| + | '''<u>Meine Lösung:</u>'''<br/> | ||
| + | <document>RitterSport_IMG.pdf</document><br/> | ||
| + | @Tchu Tcha Tcha: aha, SWS. Das ist auch ne Idee;)<br/> | ||
| + | --[[Benutzer:RitterSport|RitterSport]] 12:06, 10. Jul. 2012 (CEST) | ||
| + | |||
| + | == Anmerkungen Buchner zu den Beweisen "Umkehrung Basiswinkelsatz" von Tchu Tcha Tcha und RitterSport== | ||
| + | Zum Beweis von Tchu Tcha Tcha:<br /> | ||
| + | Sieht zwar gut aus, es gibt aber ein Probelm: Wir haben den Satz zur Innenwinkelsumme im Dreieck noch nicht. Somit kriegen Sie den Beweis so nicht hin, weil Schritt 5 können Sie anders nicht begründen.<br /><br /> | ||
| + | |||
| + | Zum Beweis von RitterSport:<br /> | ||
| + | Sieht zwar auch gut aus, aber was machen Sie, wenn <math>\left| CM \right| < \left| AM \right| bzw. \left| BM \right|</math>? Das kann ja durchaus passieren, und dann können Sie den Satz SsW nimmer anwenden...<br /> | ||
| + | <br /> | ||
| + | Ich gebe Ihnen mal eine Idee mit auf den Weg: Man könnte ja die Mittelsenkrechte m von<math>\overline{AB} </math> konstruieren. Wenn Sie jetzt zeigen, dass <math>C \in m</math> haben Sie mithilfe des Mittelsenkrechtenkriteriums die Behauptung bewiesen.<br /> | ||
| + | Also konkret:<br /> | ||
| + | Zeigen Sie, dass <math>C \in m</math> (mit Widerspruchsbeweis). | ||
| + | --[[Benutzer:Buchner|Buchner]] 16:48, 11. Jul. 2012 (CEST)<br /> | ||
| + | |||
| + | d) Lösungsversuch 2:<br /> | ||
| + | '''BEWEIS UMKEHRUNG BASISWINKELSATZ'''<br /> | ||
| + | <br />[[Datei:Zusatz 10.1.png]]<br /> | ||
| + | |||
| + | Vor.: <math>\alpha \tilde {=} \beta</math> <br /> | ||
| + | Beh.: <math>a \tilde {=} b</math> <br /> | ||
| + | Annahme: a NICHT kongruent b <br /> | ||
| + | |||
| + | 1.Fall: <math>C \not\in m_c</math> (A1)<br /> | ||
| + | |||
| + | Da nach dem Mittelsenkrechtenkriterium für alle Punkte P der Mittelsenkrechten <math>m_c</math> gilt:<br /> | ||
| + | <math>\left| PA \right| = \left| PB \right| </math><br />, muss unsere Annahme stimmen, wenn <math>C \not\in m_c</math> (A1).<br /> | ||
| + | Behauptung ist zu verwerfen.<br /> | ||
| + | |||
| + | 2.Fall: <math>C \in m_c</math> (A2)<br /> | ||
| + | |||
| + | (1) Es existiert <math>m_c</math> (die Mittelsenkrechte von <math>\overline{AB}</math> ) // Def. Mittelsenkrechte<br /> | ||
| + | (2) Wenn (A2) gilt, dann gilt nach dem Mittelsenkrechtenkriterium:<math>\left| CA \right| = \left| CB \right| </math> // (A2), Mittelsenkrechtenkriterium<br /> | ||
| + | (3) <math>a \tilde {=} b</math> // (2) <br /> | ||
| + | (4) Behauptung stimmt // (3) <br /> | ||
| + | qed.<br /> | ||
| + | Wäre dieser Beweis korrekt? --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:15, 11. Jul. 2012 (CEST) | ||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 11. Juli 2012, 20:15 Uhr
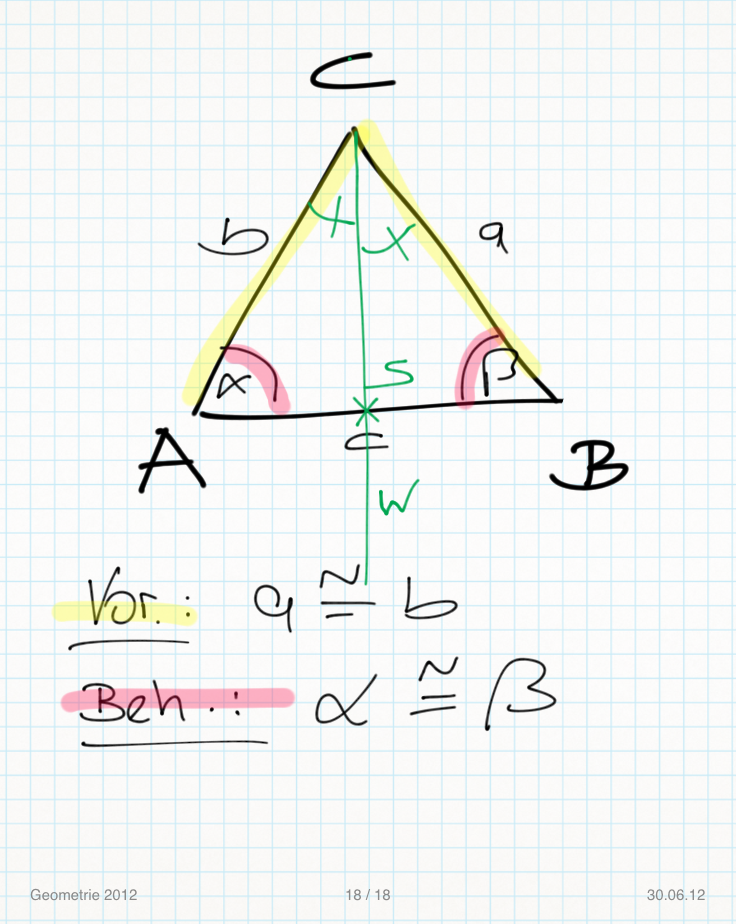
Versuch Lerngruppe Nummero6/Tchu Tcha Tcha:
a) Wenn in einem Dreieck zwei Seiten kongruent sind, dann sind die Basiswinkel kongruent.
Wenn in einem Dreieck zwei Innenwinkel kongruent sind, dann sind zwei Seiten kongruent.
Vor. 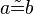
Beh.: 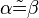
(1) 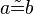 // Vor.
// Vor.
(2) es existiert w (die WH von  ) // Ex. & Eind. der WH
) // Ex. & Eind. der WH
(3) Fehler beim Parsen(Syntaxfehler): \ w \cap \overline{AB} = \{S}
// Vor., (1), Lemma 1
(4) Fehler beim Parsen(Syntaxfehler): \left| \angle ACS \right| \tilde {=} \left| \angle DCS \right| \tilde
// (2),(3), Def. WH
(5) 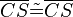 // trivial, Vor., (3)
// trivial, Vor., (3)
(6) 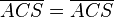 // (1),(4),(5), SWS
// (1),(4),(5), SWS
(7) 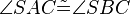 // (6), Dreieckskongruenz
// (6), Dreieckskongruenz
(8) Beh. stimmt // (7)
qed
d) BEWEIS UMKEHRUNG BASISWINKELSATZ
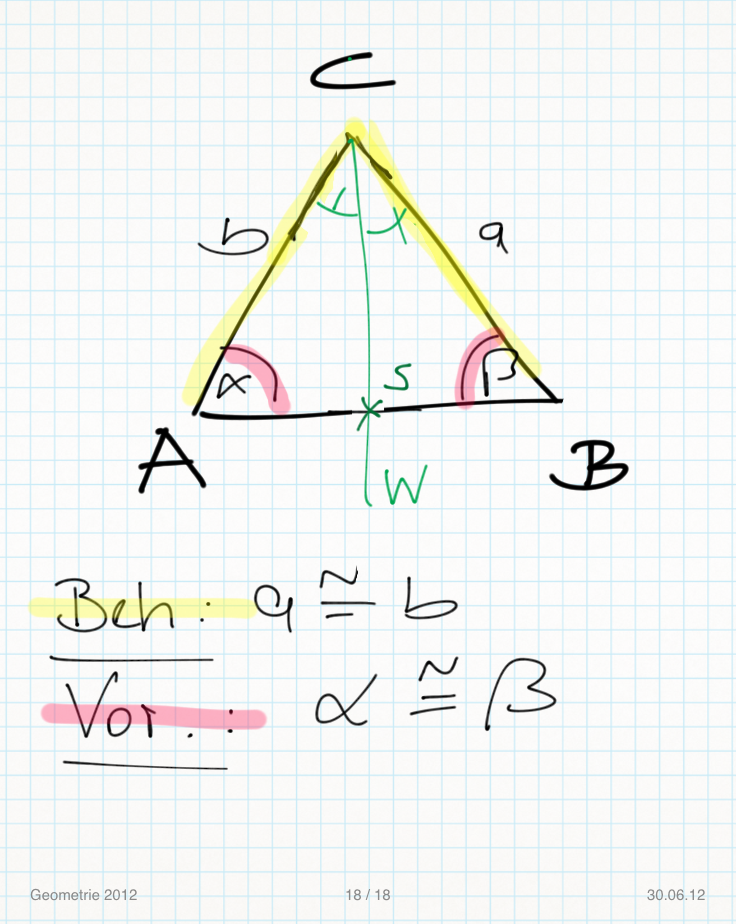
Vor.: 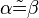
Beh.: 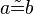
(1) 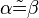 // Vor.
// Vor.
(2) es existiert w (die WH von  ) // Ex. & Eind. der WH
) // Ex. & Eind. der WH
(3) Fehler beim Parsen(Syntaxfehler): \ w \cap \overline{AB} = \{S}
// Vor., (1), Lemma 1
(4) Fehler beim Parsen(Syntaxfehler): \left| \angle ACS \right| \tilde {=} \left| \angle BCS \right| \tilde
// (2),(3), Def. WH
(5) 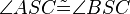 // nach Vor., (4) und Innenwinkelsumme im Dreieck
// nach Vor., (4) und Innenwinkelsumme im Dreieck
(6) 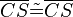 // trivial, (3)
// trivial, (3)
(7) 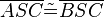 // (4),(5),(6),WSW
// (4),(5),(6),WSW
(8) 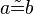 // (7), Dreieckskongruenz
// (7), Dreieckskongruenz
(9) Beh. stimmt // (8)
qed
--Tchu Tcha Tcha 13:53, 30. Jun. 2012 (CEST)
Meine Lösung:
<document>RitterSport_IMG.pdf</document>
@Tchu Tcha Tcha: aha, SWS. Das ist auch ne Idee;)
--RitterSport 12:06, 10. Jul. 2012 (CEST)
Anmerkungen Buchner zu den Beweisen "Umkehrung Basiswinkelsatz" von Tchu Tcha Tcha und RitterSport
Zum Beweis von Tchu Tcha Tcha:
Sieht zwar gut aus, es gibt aber ein Probelm: Wir haben den Satz zur Innenwinkelsumme im Dreieck noch nicht. Somit kriegen Sie den Beweis so nicht hin, weil Schritt 5 können Sie anders nicht begründen.
Zum Beweis von RitterSport:
Sieht zwar auch gut aus, aber was machen Sie, wenn 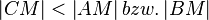 ? Das kann ja durchaus passieren, und dann können Sie den Satz SsW nimmer anwenden...
? Das kann ja durchaus passieren, und dann können Sie den Satz SsW nimmer anwenden...
Ich gebe Ihnen mal eine Idee mit auf den Weg: Man könnte ja die Mittelsenkrechte m von konstruieren. Wenn Sie jetzt zeigen, dass
konstruieren. Wenn Sie jetzt zeigen, dass 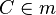 haben Sie mithilfe des Mittelsenkrechtenkriteriums die Behauptung bewiesen.
haben Sie mithilfe des Mittelsenkrechtenkriteriums die Behauptung bewiesen.
Also konkret:
Zeigen Sie, dass 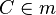 (mit Widerspruchsbeweis).
--Buchner 16:48, 11. Jul. 2012 (CEST)
(mit Widerspruchsbeweis).
--Buchner 16:48, 11. Jul. 2012 (CEST)
d) Lösungsversuch 2:
BEWEIS UMKEHRUNG BASISWINKELSATZ
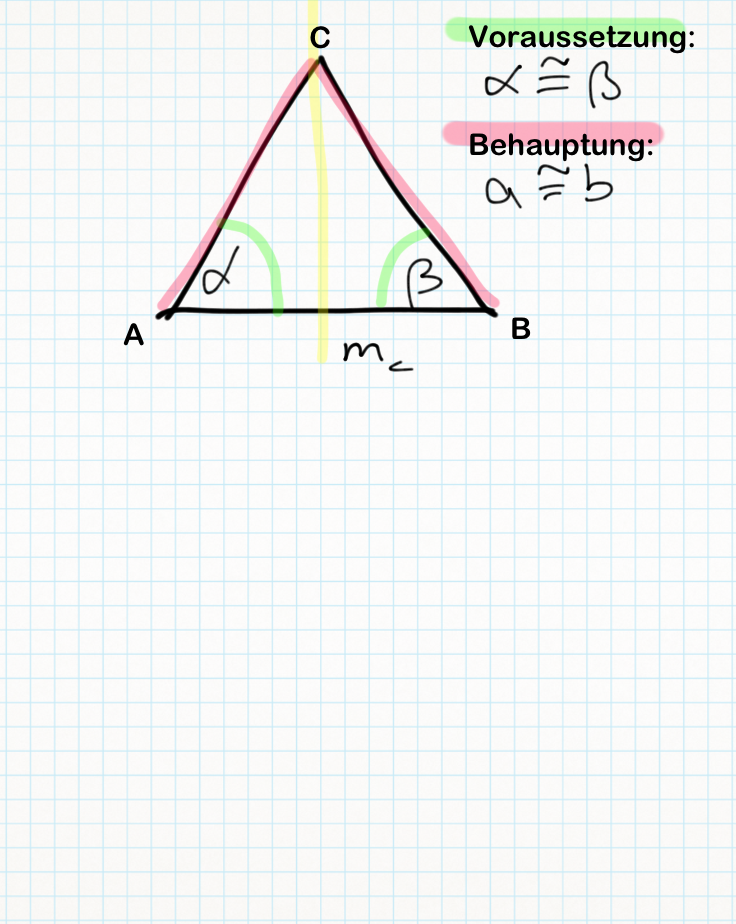
Vor.: 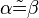
Beh.: 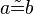
Annahme: a NICHT kongruent b
1.Fall: 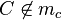 (A1)
(A1)
Da nach dem Mittelsenkrechtenkriterium für alle Punkte P der Mittelsenkrechten 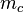 gilt:
gilt:
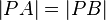
, muss unsere Annahme stimmen, wenn 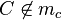 (A1).
(A1).
Behauptung ist zu verwerfen.
2.Fall: 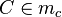 (A2)
(A2)
(1) Es existiert 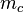 (die Mittelsenkrechte von
(die Mittelsenkrechte von  ) // Def. Mittelsenkrechte
) // Def. Mittelsenkrechte
(2) Wenn (A2) gilt, dann gilt nach dem Mittelsenkrechtenkriterium: // (A2), Mittelsenkrechtenkriterium
// (A2), Mittelsenkrechtenkriterium
(3) 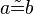 // (2)
// (2)
(4) Behauptung stimmt // (3)
qed.
Wäre dieser Beweis korrekt? --Tchu Tcha Tcha 21:15, 11. Jul. 2012 (CEST)