Lösung von Aufgabe 7.8: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Nicola (Diskussion | Beiträge) |
|||
| Zeile 3: | Zeile 3: | ||
Das Dreieck ABC ist die Summer der Strecken <math>\overline{AB}</math>, <math>\overline{BC}</math> und <math>\overline{CA}</math>. | Das Dreieck ABC ist die Summer der Strecken <math>\overline{AB}</math>, <math>\overline{BC}</math> und <math>\overline{CA}</math>. | ||
--[[Benutzer:Nicola|Nicola]] 13:52, 6. Jun. 2010 (UTC) | --[[Benutzer:Nicola|Nicola]] 13:52, 6. Jun. 2010 (UTC) | ||
| + | |||
| + | [[Lösungsversuch:]] | ||
| + | |||
| + | Gegeben seien drei paarweise verschiedene Punkte <math>\ A</math>, <math>\ B</math>, <math>\ C</math>, die nicht kolinear sind. Unter einem Dreieck <math>\overline{ABC}</math> versteht man die Vereinigungsmenge der Strecken <math>\overline{AB}</math>, <math>\overline{BC}</math> und <math>\overline{CA}</math>. Die Strecken <math>\overline{AB}</math>, <math>\overline{BC}</math> und <math>\overline{CA}</math> werden Seiten des Dreiecks <math>\overline{ABC}</math> genannt. Die Punkte <math>\ A</math>, <math>\ B</math>, <math>\ C</math> werden Eckpunkte des Dreiecks <math>\overline{ABC}</math> genannt. | ||
Version vom 9. Juni 2010, 12:44 Uhr
Unter einem Dreieck versteht man die Vereinigungsmenge von drei besonderen Strecken (umgangssprachlich: Das Dreieck ist sein Rand.). Definieren Sie den Begriff Dreieck  .
.
Das Dreieck ABC ist die Summer der Strecken  ,
,  und
und 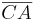 .
--Nicola 13:52, 6. Jun. 2010 (UTC)
.
--Nicola 13:52, 6. Jun. 2010 (UTC)
Gegeben seien drei paarweise verschiedene Punkte  ,
,  ,
,  , die nicht kolinear sind. Unter einem Dreieck
, die nicht kolinear sind. Unter einem Dreieck  versteht man die Vereinigungsmenge der Strecken
versteht man die Vereinigungsmenge der Strecken  ,
,  und
und 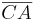 . Die Strecken
. Die Strecken  ,
,  und
und 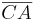 werden Seiten des Dreiecks
werden Seiten des Dreiecks  genannt. Die Punkte
genannt. Die Punkte  ,
,  ,
,  werden Eckpunkte des Dreiecks
werden Eckpunkte des Dreiecks  genannt.
genannt.

