Lösung von Aufgabe 6.2P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | | Voraussetzung || | + | | Voraussetzung || koll. (A,B,C) |
|- | |- | ||
| − | | Behauptung || ( | + | | Behauptung || Zw (A,B,C) oder Zw (B,A,C) oder Zw (A,C,B) |
|} | |} | ||
<br /> | <br /> | ||
| Zeile 20: | Zeile 20: | ||
!Beweisschritt!!Begründung | !Beweisschritt!!Begründung | ||
|- | |- | ||
| − | | 1 ( | + | | 1 koll (A,B,C)|| Voraussetzung |
|- | |- | ||
| − | | 2 | + | | 2 |AB|+|BC| = |AC| || Dreiecksungleichung, 1. |
|- | |- | ||
| − | | 3 ( | + | | 3 Zw (A,B,C) || Def. Zwischenrelation, 2. |
|} | |} | ||
<br /> | <br /> | ||
| − | + | * Das ist so nicht richtig. Schritt 2 folgt weder aus der Dreiecksungleichung noch aus 1. - also man kann den 2. Schritt überhaupt nicht so herleiten.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:04, 16. Jul. 2012 (CEST) | |
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 16. Juli 2012, 12:04 Uhr
Beweisen Sie: Es sei  mit
mit  sind paarweise verschieden.
sind paarweise verschieden.
Dann gilt genau eine der folgenden Zwischenrelationen:  oder
oder 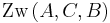 oder
oder 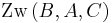 .
.
sollen wir die welt der mathematik ins wanken bringen und axiome beweisen???
oder hab ich was falsch gelesen?--Studentin 17:29, 26. Mai 2012 (CEST)
- Das war und ist so kein Axiom.--Tutorin Anne 17:24, 27. Mai 2012 (CEST)
Kann man das mit der Dreiecksungleichung beweisen/ begründen? [Schmetterling]
- Richtig, dir wird man dazu benötigen, aber nicht nur. Zu beweisen ist: Genau eine Zwischenrelation.
Hier mal ein Anfang: --Tutorin Anne 15:43, 6. Jun. 2012 (CEST)
| Voraussetzung | koll. (A,B,C) |
| Behauptung | Zw (A,B,C) oder Zw (B,A,C) oder Zw (A,C,B) |
| Beweisschritt | Begründung |
|---|---|
| 1 koll (A,B,C) | Voraussetzung |
| AB|+|BC| = |AC| | Dreiecksungleichung, 1. |
| 3 Zw (A,B,C) | Def. Zwischenrelation, 2. |
- Das ist so nicht richtig. Schritt 2 folgt weder aus der Dreiecksungleichung noch aus 1. - also man kann den 2. Schritt überhaupt nicht so herleiten.--Tutorin Anne 13:04, 16. Jul. 2012 (CEST)

