Lösung Testaufgabe 3.2: Unterschied zwischen den Versionen
| Zeile 15: | Zeile 15: | ||
Für Aufgabe 3.3 zeigen Sie jetzt, dass <math>AD \|| BC</math> ist und dass <math>\overline{AB} \tilde= \overline{CD}</math> gilt. Bleibt zu zeigen, dass <math>\overline{ABCD}</math> kein beliebiges Parallelogramm sein kann (nur Rechteck ist erlaubt).--[[Benutzer:*m.g.*|*m.g.*]] 14:33, 17. Jul. 2012 (CEST) | Für Aufgabe 3.3 zeigen Sie jetzt, dass <math>AD \|| BC</math> ist und dass <math>\overline{AB} \tilde= \overline{CD}</math> gilt. Bleibt zu zeigen, dass <math>\overline{ABCD}</math> kein beliebiges Parallelogramm sein kann (nur Rechteck ist erlaubt).--[[Benutzer:*m.g.*|*m.g.*]] 14:33, 17. Jul. 2012 (CEST) | ||
| + | |||
| + | --> Das verstehe ich nicht: Muss nun bewiesen werden, dass die Diagonalen senkrecht aufeinander stehen und das gl. Trapez ein Rechteck ist? Oder muss bewiesen werden, dass die Diagonalen im Parallelogramm NICHT senkrecht aufeinander stehen? Ich wüsste nicht, wie ich das nachweisen soll?! --[[Benutzer:*osterhase*|*osterhase*]] 18:12, 17. Jul. 2012 (CEST) | ||
Version vom 17. Juli 2012, 17:12 Uhr
Ein Viereck, das ein Sehnenviereck ist und dessen Diagonalen kongruent sind ist ein gleichschenkliges Trapez.--Tchu Tcha Tcha 11:13, 17. Jul. 2012 (CEST)
Ein Viereck mit zwei zueinander kongruenten Seiten und gleichlangen Diagonalen heißt gleichschenkliges Trapez. Ist das mit den Seiten richtig bzw. nicht eigentlich zu viel Information? Wenn diese Information aber fehlt, reicht die Definition nicht aus um in Teilaufgabe 3.3 einen gescheiten Beweis zu führen. Bitte um Hilfe! --*osterhase* 12:08, 17. Jul. 2012 (CEST)
Ein Viereck mit gleichlangen Diagonalen, die einander im selben Verhältnis schneiden, heißt gleichschenkliges Trapez. (Selbes Problem wie bei vorheriger Definition: Hilfe!) --*osterhase* 12:08, 17. Jul. 2012 (CEST)
Ein Viereck mit einem Umkreis und zwei kongruenten Diagonalen, die sich im gleichen Verhältnis schneiden, ist ein gleichschenkliges Trapez (damit würde sich ein Beweis führen lassen). --Mahe84 13:43, 17. Jul. 2012 (CEST)
--> Ich glaube das ist schon zu viel. Entweder die Geschichte mit dem Umkreis und zwei Diagonalen die sich im selben Verhältnis schneiden, oder ein Viereck mit kongruenten Diagonalen die sich im selben Verhältnis schneiden (ohne den Umkreis).--*osterhase* 17:21, 17. Jul. 2012 (CEST)
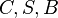sind beweglich. Alles klar?
Die Definition von Osterhase ist perfekt: Ein Viereck mit gleichlangen Diagonalen, die einander im selben Verhältnis schneiden, heißt gleichschenkliges Trapez.--*m.g.* 14:18, 17. Jul. 2012 (CEST)
Für Aufgabe 3.3 zeigen Sie jetzt, dass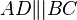 
ist und dass 
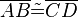gilt. Bleibt zu zeigen, dass 
kein beliebiges Parallelogramm sein kann (nur Rechteck ist erlaubt).--*m.g.* 14:33, 17. Jul. 2012 (CEST)
--> Das verstehe ich nicht: Muss nun bewiesen werden, dass die Diagonalen senkrecht aufeinander stehen und das gl. Trapez ein Rechteck ist? Oder muss bewiesen werden, dass die Diagonalen im Parallelogramm NICHT senkrecht aufeinander stehen? Ich wüsste nicht, wie ich das nachweisen soll?! --*osterhase* 18:12, 17. Jul. 2012 (CEST)
