Lösung von Aufg. 5.5P (SoSe 12): Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Jeder kann aber auch seine Ideen einscannen oder abfotografieren oder einfach als Text einstellen:--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:34, 22. Mai 2012 (CEST) | Jeder kann aber auch seine Ideen einscannen oder abfotografieren oder einfach als Text einstellen:--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:34, 22. Mai 2012 (CEST) | ||
| − | Voraussetzung: Zwei Punktmengen | + | Voraussetzung: Zwei Punktmengen Q und F, die konvex sind . |
| − | Behauptung: Der Durchschnitt zweier Punktmengen ist konvex. --[[Benutzer:Hakunamatata|Hakunamatata]] 17:56, 23. Mai 2012 (CEST) | + | Behauptung: Der Durchschnitt zweier Punktmengen Q und F ist konvex. --[[Benutzer:Hakunamatata|Hakunamatata]] 17:56, 23. Mai 2012 (CEST) |
{| class="wikitable sortable" | {| class="wikitable sortable" | ||
!Beweisschritt!!Begründung | !Beweisschritt!!Begründung | ||
|- | |- | ||
| − | | (1) || | + | | (1) <math>Q \cap F = M</math> || Vor |
|- | |- | ||
| − | | (2) || | + | | (2) M ist Teilmenge von Q und von F || Def. Schnittmenge, 1) |
|- | |- | ||
| − | | (3) || | + | | (3) Für alle A,B die Element von M sind gilt: Strecke AB ist Teilmenge von Q und von F || 2), Def.konvex |
|- | |- | ||
| − | | (4) || | + | | (4) Strecke AB ist Teilmenge von M || 2),3) Def. Schnittmenge |
| + | |- | ||
| + | | (5) M ist konvex || 4), Def. konvex | ||
|} | |} | ||
| − | + | -- Steffem (16.07.12) Habs mal versucht.<br /> | |
| + | Sehr Gut! Zwei Kleinigkeiten: Bei Schritt 1 habe ich korrigiet, geschnitten statt vereinigt. Und bei Schritt 4 habe ich Def. Schnittmenge noch ergänzt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:47, 18. Jul. 2012 (CEST) | ||
Aktuelle Version vom 18. Juli 2012, 13:47 Uhr
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Ich gebe mal einen Anfang vor, damit es mit dem Formatieren einfacher ist. Möge jemand anderes weitermachen z.B. mit der Voraussetzung und Behauptung.
Jeder kann aber auch seine Ideen einscannen oder abfotografieren oder einfach als Text einstellen:--Tutorin Anne 18:34, 22. Mai 2012 (CEST)
Voraussetzung: Zwei Punktmengen Q und F, die konvex sind . Behauptung: Der Durchschnitt zweier Punktmengen Q und F ist konvex. --Hakunamatata 17:56, 23. Mai 2012 (CEST)
| Beweisschritt | Begründung |
|---|---|
(1) 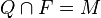 |
Vor |
| (2) M ist Teilmenge von Q und von F | Def. Schnittmenge, 1) |
| (3) Für alle A,B die Element von M sind gilt: Strecke AB ist Teilmenge von Q und von F | 2), Def.konvex |
| (4) Strecke AB ist Teilmenge von M | 2),3) Def. Schnittmenge |
| (5) M ist konvex | 4), Def. konvex |
-- Steffem (16.07.12) Habs mal versucht.
Sehr Gut! Zwei Kleinigkeiten: Bei Schritt 1 habe ich korrigiet, geschnitten statt vereinigt. Und bei Schritt 4 habe ich Def. Schnittmenge noch ergänzt.--Tutorin Anne 14:47, 18. Jul. 2012 (CEST)
Wie fange ich denn jetzt an??? Ich finde es immer so schwer, den ersten Beweisschritt zu finden!!! Fange ich immer zuerst an, die Voraussetzung zu betrachten, oder fange ich von der Behauptung an zu beweisen??? Oder von der Annahme, wenn ich eine haben sollte???
- Joker
- Gute Fragen! Es ist richtig, zunächst die Voraussetzung zu betrachten und sich zu überlegen, welche Definitionen und Sätze könnten mir nützlich sein (Welche Begriffe stehen denn in der Voraussetzung?). Genauso schaut man sich aber auch die Behauptung an. Man kann auch von hinten beginnen und sich so von beiden Seiten an das Ergebnis nahen. Was brauche ich, was heißt es, der Durschnitt zweier Punktmengen ist konvex? Zum Beweisen darf aber die Behauptung nicht als Begründung verwendet werden. Natürlich aber Vorausssetzung und gegebenfalls auch die Annahme.
- Konkret: Wie ist der Durchschnitt definiert? Was bedeutet konvex und wie ist es definiert?--Tutorin Anne 17:35, 27. Mai 2012 (CEST)

