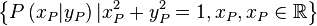Kreise 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
||
| Zeile 5: | Zeile 5: | ||
<ggb_applet width="1041" height="592" version="4.0" ggbBase64="UEsDBBQACAAIAF1lUEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAF1lUEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVbbjts2EH1OvmKg56zNqy6BnaAJECDANi2waZH2jZJom11ZNCTK9gb5+A5JySsnTZEgRQHLJMXDOTOjOSRXL8/7Bo66641t1wldkAR0W9natNt1MrjNTZ68fPF0tdV2q8tOwcZ2e+XWifBIU6+TslCbVBTkhpEqvxGaqJtcbOQNFYSLUhRcMJoAnHvzvLXv1F73B1Xpu2qn9+rWVsoF4p1zh+fL5el0WkxUC9ttl9ttuTj3dQLoZtuvk7HzHM1dLTrxAGeE0OWHn2+j+RvT9k61lU7AhzCYF0+frE6mre0JTqZ2OwyYiCKBnTbbHQaVFjhYetQBM3LQlTNH3ePa2TAE7faHJMBU6+efxB40l3gSqM3R1LpbJ2RBac5IltO0SHMpqEgTsJ3RrRvBdCRdTuZWR6NP0a7vBUqRgLO2KZU3CZ8+ASOMwDPf0NgwbNI0TpH4jvDYsNiI2MiIEXG5iFARMSJiBE/gaHpTNnqdbFTTYw5Nu+nw+13GvXtodPBnfPEYPn2GMfXmI4I5wUKJSffpJs/8k+Ij/MTyOkg6Y3Xd8J2kE2VB2bdTsh+h5BMlZeJLSia/EmX6L8mNPnxLmFTOMotU4ReeLxg5+w7GOP4xwlT8LyGulpNSVqM4oN957Pglnd73Xi68AFn4qqcgURpphkUugRbYZAxQDEAlCIlDmkPq2wx4hhMCOOTgcZRD0IbM8U9kwVgKEo35txlKEigSCZAcaJCUABQSBFmiRBlHhJQgcZGnp8yb4CmIFEc8B4E+ekVmFIEcF+IY6RlwCtwvphmwFFJvjwqv9DT3rqNJBimBlHqDKGoUdBQz4nPgPpp0TJdpD4O7SlG1r6eus4fLt0A0bkePu17cnq42xSerRpW6wYPizn9JgKNqvCIC0ca2Di7aiO+2nTrsTNXfaedwVQ9/qaO6VU6f3yC6n7gDtrJt/2tn3WvbDPu2B6hsQy4+24bO+uziNQ74bELMJ+RsIp31s3/ktTgDQ6+R33b9BFd1/dYjHrcGzOQvbfPwqtPq/mDNdRirZThzVnqoGlMb1f6OxepZfF5gOoLCbjWdQBIPh9ER29V3Dz1WMJz/1J3FE0CyRZZRkTPJM8p4nsBDnGEpW+Sc0IzlMmWCZehZpbz0GFsQTjKeFXj8ZIyjLB++MlVEYn28fB911pfQt52p5/23/Svb1JdEhNhfq4MbunBzwI2x8xH91G4bHeoj7LR4LFf3pT3fxcLg0db7hwOOSOQvtyHngPsCkxIBY1vGNmC8YxcUCRgSEGSqNFNf5mnBAiK0ZWwDCks3ujYGSqcoKZloTB92M5JcaSbUvT/jh9a422ngTHU/Rkoj/t2wL/Wleq5N0v/MpPcZbxu9+zDe33z/j1n//U475e8hknFZ5Fkm8Z8VeR5r9LPqXN3rrtXNKAYshMEOfdT2TCe1rsweh3FiTKjyH/s3DCC+rfW201PcTbjTxXSHWTKv8y9eB1NvOrt/2x7fYyV95sBqOXm56qvOHHy9QokHyL1+rEmMXeH5U8/XefVi6ip/zmB6nU8t6npwO9uFWxtuR9h6hjk0aHm8l774G1BLBwiMEWu6mQQAADQLAABQSwECFAAUAAgACABdZVBB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAF1lUEGMEWu6mQQAADQLAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAMAUAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> | <ggb_applet width="1041" height="592" version="4.0" ggbBase64="UEsDBBQACAAIAF1lUEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAF1lUEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVbbjts2EH1OvmKg56zNqy6BnaAJECDANi2waZH2jZJom11ZNCTK9gb5+A5JySsnTZEgRQHLJMXDOTOjOSRXL8/7Bo66641t1wldkAR0W9natNt1MrjNTZ68fPF0tdV2q8tOwcZ2e+XWifBIU6+TslCbVBTkhpEqvxGaqJtcbOQNFYSLUhRcMJoAnHvzvLXv1F73B1Xpu2qn9+rWVsoF4p1zh+fL5el0WkxUC9ttl9ttuTj3dQLoZtuvk7HzHM1dLTrxAGeE0OWHn2+j+RvT9k61lU7AhzCYF0+frE6mre0JTqZ2OwyYiCKBnTbbHQaVFjhYetQBM3LQlTNH3ePa2TAE7faHJMBU6+efxB40l3gSqM3R1LpbJ2RBac5IltO0SHMpqEgTsJ3RrRvBdCRdTuZWR6NP0a7vBUqRgLO2KZU3CZ8+ASOMwDPf0NgwbNI0TpH4jvDYsNiI2MiIEXG5iFARMSJiBE/gaHpTNnqdbFTTYw5Nu+nw+13GvXtodPBnfPEYPn2GMfXmI4I5wUKJSffpJs/8k+Ij/MTyOkg6Y3Xd8J2kE2VB2bdTsh+h5BMlZeJLSia/EmX6L8mNPnxLmFTOMotU4ReeLxg5+w7GOP4xwlT8LyGulpNSVqM4oN957Pglnd73Xi68AFn4qqcgURpphkUugRbYZAxQDEAlCIlDmkPq2wx4hhMCOOTgcZRD0IbM8U9kwVgKEo35txlKEigSCZAcaJCUABQSBFmiRBlHhJQgcZGnp8yb4CmIFEc8B4E+ekVmFIEcF+IY6RlwCtwvphmwFFJvjwqv9DT3rqNJBimBlHqDKGoUdBQz4nPgPpp0TJdpD4O7SlG1r6eus4fLt0A0bkePu17cnq42xSerRpW6wYPizn9JgKNqvCIC0ca2Di7aiO+2nTrsTNXfaedwVQ9/qaO6VU6f3yC6n7gDtrJt/2tn3WvbDPu2B6hsQy4+24bO+uziNQ74bELMJ+RsIp31s3/ktTgDQ6+R33b9BFd1/dYjHrcGzOQvbfPwqtPq/mDNdRirZThzVnqoGlMb1f6OxepZfF5gOoLCbjWdQBIPh9ER29V3Dz1WMJz/1J3FE0CyRZZRkTPJM8p4nsBDnGEpW+Sc0IzlMmWCZehZpbz0GFsQTjKeFXj8ZIyjLB++MlVEYn28fB911pfQt52p5/23/Svb1JdEhNhfq4MbunBzwI2x8xH91G4bHeoj7LR4LFf3pT3fxcLg0db7hwOOSOQvtyHngPsCkxIBY1vGNmC8YxcUCRgSEGSqNFNf5mnBAiK0ZWwDCks3ujYGSqcoKZloTB92M5JcaSbUvT/jh9a422ngTHU/Rkoj/t2wL/Wleq5N0v/MpPcZbxu9+zDe33z/j1n//U475e8hknFZ5Fkm8Z8VeR5r9LPqXN3rrtXNKAYshMEOfdT2TCe1rsweh3FiTKjyH/s3DCC+rfW201PcTbjTxXSHWTKv8y9eB1NvOrt/2x7fYyV95sBqOXm56qvOHHy9QokHyL1+rEmMXeH5U8/XefVi6ip/zmB6nU8t6npwO9uFWxtuR9h6hjk0aHm8l774G1BLBwiMEWu6mQQAADQLAABQSwECFAAUAAgACABdZVBB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAF1lUEGMEWu6mQQAADQLAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAMAUAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> | ||
==Aufgabe 1== | ==Aufgabe 1== | ||
| − | + | Lassen Sie die folgenden Punktmengen in der obigen Geogebraapplikation grafisch darstellen. Um was für geometrische Objekte handelt es ich in jedem Fall? Begründen Sie Ihre Antwort. | |
| + | # <math>\left\{P\left(x_P|y_P\right)|x_P^2+y_P^2=1, x_P,x_P \in \mathbb{R} \right\}</math> | ||
Version vom 16. Oktober 2012, 12:48 Uhr
Aufgaben zum Einstieg
Aufgabe 1Lassen Sie die folgenden Punktmengen in der obigen Geogebraapplikation grafisch darstellen. Um was für geometrische Objekte handelt es ich in jedem Fall? Begründen Sie Ihre Antwort.
|