Kreise 2012 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→DerAlgorithmus von Bresenham) |
||
| (30 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#B9D0F0; padding:1em" | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| + | =Aufgaben zum Einstieg= | ||
| + | <ggb_applet width="1041" height="592" version="4.0" ggbBase64="UEsDBBQACAAIAF1lUEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAF1lUEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVbbjts2EH1OvmKg56zNqy6BnaAJECDANi2waZH2jZJom11ZNCTK9gb5+A5JySsnTZEgRQHLJMXDOTOjOSRXL8/7Bo66641t1wldkAR0W9natNt1MrjNTZ68fPF0tdV2q8tOwcZ2e+XWifBIU6+TslCbVBTkhpEqvxGaqJtcbOQNFYSLUhRcMJoAnHvzvLXv1F73B1Xpu2qn9+rWVsoF4p1zh+fL5el0WkxUC9ttl9ttuTj3dQLoZtuvk7HzHM1dLTrxAGeE0OWHn2+j+RvT9k61lU7AhzCYF0+frE6mre0JTqZ2OwyYiCKBnTbbHQaVFjhYetQBM3LQlTNH3ePa2TAE7faHJMBU6+efxB40l3gSqM3R1LpbJ2RBac5IltO0SHMpqEgTsJ3RrRvBdCRdTuZWR6NP0a7vBUqRgLO2KZU3CZ8+ASOMwDPf0NgwbNI0TpH4jvDYsNiI2MiIEXG5iFARMSJiBE/gaHpTNnqdbFTTYw5Nu+nw+13GvXtodPBnfPEYPn2GMfXmI4I5wUKJSffpJs/8k+Ij/MTyOkg6Y3Xd8J2kE2VB2bdTsh+h5BMlZeJLSia/EmX6L8mNPnxLmFTOMotU4ReeLxg5+w7GOP4xwlT8LyGulpNSVqM4oN957Pglnd73Xi68AFn4qqcgURpphkUugRbYZAxQDEAlCIlDmkPq2wx4hhMCOOTgcZRD0IbM8U9kwVgKEo35txlKEigSCZAcaJCUABQSBFmiRBlHhJQgcZGnp8yb4CmIFEc8B4E+ekVmFIEcF+IY6RlwCtwvphmwFFJvjwqv9DT3rqNJBimBlHqDKGoUdBQz4nPgPpp0TJdpD4O7SlG1r6eus4fLt0A0bkePu17cnq42xSerRpW6wYPizn9JgKNqvCIC0ca2Di7aiO+2nTrsTNXfaedwVQ9/qaO6VU6f3yC6n7gDtrJt/2tn3WvbDPu2B6hsQy4+24bO+uziNQ74bELMJ+RsIp31s3/ktTgDQ6+R33b9BFd1/dYjHrcGzOQvbfPwqtPq/mDNdRirZThzVnqoGlMb1f6OxepZfF5gOoLCbjWdQBIPh9ER29V3Dz1WMJz/1J3FE0CyRZZRkTPJM8p4nsBDnGEpW+Sc0IzlMmWCZehZpbz0GFsQTjKeFXj8ZIyjLB++MlVEYn28fB911pfQt52p5/23/Svb1JdEhNhfq4MbunBzwI2x8xH91G4bHeoj7LR4LFf3pT3fxcLg0db7hwOOSOQvtyHngPsCkxIBY1vGNmC8YxcUCRgSEGSqNFNf5mnBAiK0ZWwDCks3ujYGSqcoKZloTB92M5JcaSbUvT/jh9a422ngTHU/Rkoj/t2wL/Wleq5N0v/MpPcZbxu9+zDe33z/j1n//U475e8hknFZ5Fkm8Z8VeR5r9LPqXN3rrtXNKAYshMEOfdT2TCe1rsweh3FiTKjyH/s3DCC+rfW201PcTbjTxXSHWTKv8y9eB1NvOrt/2x7fYyV95sBqOXm56qvOHHy9QokHyL1+rEmMXeH5U8/XefVi6ip/zmB6nU8t6npwO9uFWxtuR9h6hjk0aHm8l774G1BLBwiMEWu6mQQAADQLAABQSwECFAAUAAgACABdZVBB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAF1lUEGMEWu6mQQAADQLAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAMAUAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> | ||
| + | ==Aufgabe 1== | ||
| + | Lassen Sie die folgenden Punktmengen in der obigen Geogebraapplikation grafisch darstellen. Um was für geometrische Objekte handelt es ich in jedem Fall? Begründen Sie Ihre Antwort. | ||
| + | # <math>\left\{P\left(x_P|y_P\right)|x_P^2+y_P^2=1, x_P,x_P \in \mathbb{R} \right\}</math> | ||
| + | # <math>\left\{P\left(x_P|y_P\right)|\left(x_P-3\right)^2+\left(y_P-2\right)^2=5^2, x_P,y_P \in \mathbb{R}\right\}</math> | ||
| + | ==Aufgabe 2== | ||
| + | Lassen Sie die folgenden Kreise mittels Geoegebra grafisch darstellen, indem Sie jeweils eine entsprechende Gleichung in die Eingabezeile eintragen. | ||
| + | # Mittelpunkt: <math>M(0|0)</math> Radius: <math>r=5</math> | ||
| + | # Mittelpunkt: <math>A(2|2)</math> Radius: <math>r=4</math> | ||
| + | =Kreise in der synthetischen Geometrie= | ||
| + | ==Vereinbarung== | ||
| + | Alle unsere folgenden Betrachtungen beziehen sich auf die Geometrie in der Ebene. | ||
| + | ==Kreisdefinition== | ||
| + | {{Definition|1=Es seien <math>M</math> ein Punkt und <math>r</math> eine positive reelle Zahl. Unter dem Kreis mit dem Mittelpunkt <math>M</math> und dem radius <math>r</math> versteht man ...}} | ||
| + | =Abstände von Punkten= | ||
| + | <ggb_applet width="1031" height="697" version="4.0" ggbBase64="UEsDBBQACAAIACxYWEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIACxYWEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vr9bts4Ev+7+xSEbrFo0domRVEfrd1FEmCxBbLb4po79O56LSiJdrSRJVekE3tv+1D3IvdMNyQlRbIdx2m7zeIOqEtSHHJmfvPBoZTx96t5ji5FJbOymDhkiB0kiqRMs2I2cZZqOgid759/M56JcibiiqNpWc25mjiepszSiRNSHKYRjwcMT72BxxJ/wMM0GbAkimkoWDiNYgehlcyeFuXPfC7kgifidXIu5vy0TLgyjM+VWjwdja6uroYNq2FZzUazWTxcydRBIGYhJ07deQrb9RZdUUPuYkxGb346tdsPskIqXiTCQVqFZfb8mwfjq6xIyyt0laXqHBTGNHLQuchm56BUSFwHjTTVAhBZiERll0LC2s7QKK3mC8eQ8ULPP7A9lLf6OCjNLrNUVBMHD0kUUMwIJpiFAXB0UFllolA1Lal5jprdxpeZuLLb6p7h6DlIlWUec70j+u035GIXoye6IbZxofF9O4XtM0xt49rGsw2zNJ5d7llSz9J4lsYDGS8zmcW5mDhTnkuAMCumFZivHUu1zoWRp35wrT15AjrJ7Fcgphj8xGKu0cZP9M+Hn6cnRn0lSYerqpZ3ZNqwBITJ4Tzdz9KUNkxdzLZ5uuwGPf09TK3iBynKOtgCK/PP/LY40n1qbnK0489j6HtfRcXxqImVcR0eSJ5r2tp9lJhLHTA0QizSfk8Qg+DwA3BzhkgETeAiCAdEGPIYDEmIfN0GiAYw4SGKQqTpCEUmOlgI/3mB2cxHDDbTTwMISkSAkYcYRcQElYcglJAJTAhSlwIFY4jBIs2euHoL6iPPhxENkQcy6pgMCBBSWAhjYO8iShDVi0mAXB/5ej/i6Vj3Qy06bOkiHyOf6A0hrCGkbTgDfYio1sav4cqKxVL1IErmadNV5aK1BVBDQrpOezZB9bLig3HOY5HDSfFaWxKhS57riDCMpmWhUGPE0D6bVXxxniXytVAKVkn0C7/kp1yJ1Q9ALRvehjYpC/mqKtVJmS/nhUQoKXPcylzmpNN3W6lhQDsTXneCdSb8Tj/YybeEGbSUAviXlWzIeZq+0BTXqQGQfFnk6+NK8ItFmfXVGI/MoTMWyyTP0owXfwVn1Vw0LqhzBpHrM8inrJGkrNLXawkujFZ/F1UJARB5wwhCgtIIh57HIOWs7QxlZBi5AXZ9j9Aw9EKYkgnXwcfYkBIfB0FIPDdgzAdfWN80Z1mLy9ZEfCVa7WdVlnb7L+RxmactFkb9E75Qy8pUD5AbK63TUTHLhXERk23haE4u4nL12voGtXudrRcwwpZ/PDOwI0gNrlZyVrexbQ2NFqylwoYGGwrcOFuWtvMkcg2FaWPbGirwXitarShptCS4YZNJk9Cw0wsb4/r6nF8WmTptBipLLmpNiaX/eTmPRetA/S3JF9tSywwVh1Rv6hpO9//W6Z+dC8V1LcJcyqIwAFtHoRuFoXXTDQcdX4iqEHkdD+AIy3IpbXh3QiUVSTaHoZ2oAeXa2H8BBezTVMwq0eidm7rOwm1mcdfTtx6brX6oyvmL4vIMPGlDgPGokXIskypbaH9FMZwhF+LaJ0F3DkdQ2l2nAxigS/RRA/AqDS2E9lKdl5Wp3CAjQavjNhdzqNOQMs5p/Ls105EpALU9UBn/Aklxw4zXxoHpnY5qXJrni3NjmFrpnK9F1YPB7PdyOpVCoZUuNCB8J86AuJ3pn8q0xo402IFpjIKQPxamCAXnWQhh3c4qBJ0F8DPB2kuBYA5peA0tM6rbX6072fJYQ6EDuJfz7dMNO4JzWRRvwfP4nvAcmHwIOgS/P54DWgM6cL8UoqtFJaS+vDU4rd4fwRVuBTKuHh49sgd5H/diORdVljjdFebWwfNlzcdtxLoJa9xBmtwu1LoVan2gUOttoegXFmr1/rhF6vhApI43hRp8aanWrVTrA6Va75Dq8wyYlPM5L1JUmGr9ZQWZcVYWPD+F09K5LiM51mkQcajFVkdwqNUcl6qZlGBEs3W94ZYq+vht9ZDvd+TU5mpgSTpRdYhi+3PAdZDjrUAldaDiOk5bPK8LBgWl7AVc2KWpauoMgG3vxyxNRdFmD/GhsGukPciz+SLPkkx9Bu7HFvca4R7q8Xv3Dqhr6j8K6rhJj6SGfXAfuN+M9jbWyZ2wTnZh3TvlvhrUrIaaNUize0D6RaGgkAUUNuDWPnmje5/sB7xfVZx8UlWhX17MbBPb5s5lRWDQdaN9RcV2ofXF6oI+zq/KfA2JZLdTn0Dj7vJtuAvkcFUjloxbshgauGIntxnBMmxgbre63cF2+9edI4YwamzIyO7j7tCgubl8lWKmR60g/JNcbY+cB1ewzPgO8Q7zNbwR+QQfFvl3D3zjTbmuh9tAh0Jn+yJ5IcRC3/9fFmcVL6T+xGBpGsgON0L8dY2wB+Y2w+L/RZyTe3N2L7SZcu917doMjRUGjbsfeM79QazQz+PmTdruArzO4sdbWfw//96fqs1bltZuQL1xlSBDFuAg8qnrB5EXRr7/iRnZ1jAE33D/OCDGtt7ZHW44XiWdQ7R5wZTn5dWfxTQXK4PsnmDYuqadiZUi9UXtuw/LUj379rs/EfyMT+A6PYCLIpq8zcVUPbST6DF6eMrPxJt/wPQ/H8Gwfv7WvCJ9NLiJ+HgH8QTt2BQNUJ/67bO6s+sOqUB8p6/LfRammTR69A1Qf0SQcNmdtt+MzEtj7DQBWK+XilfqlS6KkEkS0TDyqMei0KckcFkU1Sde5PnEi2CMSRCyoFtq3W5ut29uUHkNpl5rU6Pd5lv3bL3f1Ou+8WpL79gRDN2nNX737R1sfb+XkN/B1sz1iI9D6oV+qD8orPXfJ0QeC3zfJWBsSjzvbramG7ZOJm/lh0r9i79zH8fv3I+oHm/ah3fsAqSb03Fv+iP4jdllK575u4fuow7t4y2KeIPi45arJJ3Zu3gH/T/wDrrhHexG9xh1vxaYL3r1n6c8/y9QSwcISQsSt6sIAAA7IwAAUEsBAhQAFAAIAAgALFhYQdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAsWFhBSQsSt6sIAAA7IwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAEIJAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> | ||
| + | <br /><br /> | ||
| + | Wir beziehen uns auf die obigen Punkte <math>A\left(x_A,y_A\right)</math> und <math>B\left(x_B,y_B\right)</math>.<br /> | ||
| + | Der Punkt <math>C </math> ist der Schnittpunkt der Senkrechten durch <math>A</math> auf die x-Achse mit der Senkrechten von <math>B</math> auf die y-Achse.<br /> Der Punkt <math>C</math> hat damit die Koordinaten <math>\left(x_A-x_B|y_A-y_B\right)</math>. | ||
| + | <br /> | ||
| + | Das Dreieck <math>\overline{ABC}</math> ist rechtwinklig. Nach dem Satz des Pythagoras gilt:<br /> | ||
| + | (I) <math>|AB|^2=|AC|^2+|BC|^2</math><br /> | ||
| + | Unter Berücksichtigung der Koordinaten von <math>A, B, C</math> schreibt sich (I) wie folgt:<br /> | ||
| + | (II) <math>|AB|^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2</math><br /><br /> | ||
| + | Abstand zweier Punkte: | ||
| + | {| class="wikitable" | ||
| + | | <math>|AB|=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}</math> | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | =Analytische Beschreibung von Kreisen mittels des Satzes von Pythagoras= | ||
| + | ==Kreis in Mittelpunktslage== | ||
| + | <ggb_applet width="1031" height="697" version="4.0" ggbBase64="UEsDBBQACAAIAChcWEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAChcWEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vr/b9s2Fv+5+ysIYRhaLLZJfXfP6aAVGK5AugZI7tDtcC1oibY5y5In0Y4V7I+/R1KSJUvxkjjtbgmakCKf+L583uN7z+7kh90qRluW5TxNzg0yxAZiSZhGPJmfGxsxG/jGD2++mcxZOmfTjKJZmq2oODdsScmjc8N0pz6mtjnAXkQHNvbZYBxabOBQRqb+1HcpmxoI7XL+Okl/piuWr2nIrsIFW9GLNKRCMV4IsX49Gt3c3AwrVsM0m4/m8+lwl0cGAjGT/NwoJ6/huNZLN5YiNzEmo4/vL/TxA57kgiYhM5BUYcPffPNicsOTKL1BNzwSC1AYW2MDLRifL0Apn5gGGkmqNVhkzULBtyyHdxuPSmmxWhuKjCZy/4WeobjWx0AR3/KIZecGHpKxZ2GHYIId3wOOBkozzhJR0pKS56g6bbLl7EYfK2eKo20gkabxlMoT0R9/IBObGJ3JgejBhMF19RbWa9jSg6kHWw+OprH167YmtTWNrWlskHHLcz6N2bkxo3EOJuTJLAP46udcFDFT8pQLe+3JGeiU81sgtjD4iba5tDY+k78u/NpyY9RWkjS4imzzQKYVS7AwuT9P8yRNrYqpiZ0uT9O5Q0/3CFOt+L0UdRq2BVbqn/rtcLSOqXnIUT+fxtC1v4qKk1EVK5MyPFC+kLSl+wi2ymXAWGPkjKXfE+RAcLgeuLmDyBgGz0QQDog4yHbgkfjIlaOHLA82bGQhH0k6YiEVHY4Pf2xPHeYiBw6Tqx4EJSLAyEaOhYgKKhtBKCEVmBCkpgUUjoMceEmyJ6Y8wnKR7cKT5SMbZJQx6REgtOBFeAb2JrIIsuTLxEOmi1x5HrFlrLu+FB2ONJGLkUvkgRDWENI6nIHeR5bUxi3NxZP1RrRMFK6iairSdY0FUMOFtL/29AXVuhVfTGI6ZTFkiiuJJEJbGsuIUIxmaSJQBaKv1+YZXS94mF8xIeCtHP1Gt/SCCrb7CajzireiDdMkv8xS8TaNN6skRyhMY1zLnMakMTdrqeHBamzYzQ2nseE25l4v3xR20CZnwD/N8oqcRtE7SbG/GsCSH5K4+DFjdLlOeVuNyUglnQnbhDGPOE3+Dc4quUi7oEYOIvsc5FpOJUmaRVdFDi6Mdr+yLIUk4I2H4+YPBFmhtyzLkhk5D6kMOAcPcfMHzi/KLfvgiBIbtq1RoTtWKzzPeNScv8t/TOOoVl9p/JauxSZTBQNch5lUI0jmMVNeoS5YyMbhcprurrQ7WPqs62INT1jzn86VpRHcBqYDV+m8HKd6VDRSsJoKKxqsKHDlXzyq98nYVBRqnOpRUYHDatFKRUmlJcEVG56rOwwbrUhR3i5T+ybh4qJ6EDxclpoSTf/zZjVltc+0jyRPdqSUGYqMXHwsyzY5/6Uxv14wQWX54ZiWM/Y9z4G/5tj3tWce+ORkybKExWUIgCNs0k2uI7oRHREL+Qoe9UZpUCrB/hcooFcjNs9YpXesSjltbrWLm87dWVZH/ZSlq3fJ9ho86UCAyaiScpKHGV9Lf0VTSBtLtvdJ0J1C1oma78mYBdOFMruAeYU0LUTzRizSTBVrcAnBKEM1ZisozZBQzplsVizjYQ1Upqo+EGpTym0NSyNIlFA6/Q1uxwNw95DB9h3ui2i8XiiwSOmktGBZyzTqtPdpVDIu6fJYFploxXXSXNGd8mNEpzlcnALqbMAi2dfZWrLy4oEsKp1lJ6s0OSn0xWGgGd81DAo24rfgE7SlzD6MBNzpS6hccxXrooxqNfknjyKW1NLSBLxHYQC32lqriyCjMB0Z9atrUF/dJw3kS2A6EKkrqDb2e+NUMNStU8OBj8LxYTbLmZAGHBBH2c+2j6F1L/1Jn/5lxOSSV4WVGm91xOumRZpC3rGtTKxXD0Ktac8wXa1oEqFE1WZveRbGzNgXCxRLsyJKpPtr021EtbHUh5VHdMCBuGtEz/JkcPAjoDFtZa0BIcegeYw7Q8ZmyRb0gAoBOlxcXr4FrrCpVnZgu4GGjZRLt6QBHDhFxncoqOiDiiowpeB4aNrNbA5iBVbJI7CrowOnnGnZfk+0OrlOJLJu4zMA4wHBdPkXBZMGzPnykWQNieZlDt0vEEpXbC7X+2PpshNL9Hgs5eVplfXpn6DT0Pj0cNoDgA+NOFDGKypr3jYPe0xQHTguX61jHnJRmyuWgL5LBNRDTCX0bpmyZGwtq8sPyXVGk1x+ZqVpKo9tRcBunYFg0pdKy+0+XxoIlmH28vKV7oWO1wXyjU5lQOwHpv3jUhW1VMU9pSq6UkmsnlKoa7YTpBTru983qfjHtwiMca7n6Hv08oJes4//gbX/voLHcv1MEn0y+8g+vTRfNUi/1UOfutA37qNBC/JXRgTPlQ5tRysb4RxwmdWfe6guCBuVh5fv54Jm4lLeMEiFlT/EpN2oqQJj6Bzmgv299edYWV2sPpnfFwoMdAcasFCchIv1rHDxhuNDBFQGGVutvvphuNgHuGR9eGQN+/cET3YCRPYzg8jXKYkMiddCxbsLlnbmVmcd5O1lJ2EHxxN2u5gKHlVMEVN/FqLGRxdU2hjjr1FQYc/1Pde1TNvBrmU7Zafie2MCW3hsegT+el+72go64E0fVm1N/1+qrT5bFv2WfxalWFCXYsE9S7GgW4p1bPO0hVlQF2b3k7HoytgD6wkyHmvqPveUSdUXMF+ir/tCV83AGfo69Q7sqvE49ULp8z+ybwU+k3t6IDlEVwv7tE5H9t3APQUregSzn7pNUYX4525PEPQU+8FhTxD09gTBKT1Bn7v/rUubdvXplB9uDbHTrHPcOwudfsTMDmJFD2JFC7GzohevooMXeghg5jMHTNdiA3OI3QdC1AGo22YXrTb7rOhtsrvN3MMAelbwQJdtHTQIqpry/Nb3pw/Eyuq7AFWjHfQ32kHdaJ9y2VnPPHbGOnagnnPv9RnIqPm9n/o6vvy/ZW/+B1BLBwiJKwxZqggAAPgmAABQSwECFAAUAAgACAAoXFhB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAChcWEGJKwxZqggAAPgmAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAQQkAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> | ||
| + | |||
| + | <br /><br /> | ||
| + | Kreis <math>k</math> in Mittelpunktslage, Radius:r<br /><br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |||
| + | |||
| + | | <math>k=\left{A\left(x_A|y_A\right)|x_A^2+y_A^2=r^2\right}</math> | ||
| + | |- | ||
| + | |||
| + | |} | ||
| + | |||
| + | ==allgemeine Lage== | ||
| + | =DerAlgorithmus von Bresenham= | ||
| + | <ggb_applet width="997" height="728" version="4.0" ggbBase64="UEsDBBQACAAIAFhCYUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFhCYUEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Z3dcttGlsevZ56iS5NKJTOUjP4AQCb2TEkABDtxEsd2nKns7KYoEZIwpkgNSdlSPh5gn2Jv9hn2au/mTfZJ9jSAboLqJtFtkg1ys1UJSZMgef7ndJ9/g2L/+Pgvd9dD9C6bTPPx6MkBPvIOUDY6Hw/y0eWTg9vZxWH34C9//v3jy2x8mZ1N+uhiPLnuz54cMH5kPnhyEDJMPYKzwx5jwSE7p2eHZ5TB8y5C1qfdAO44O0Dobpp/Nhp/3b/Opjf98+zV+VV23X8+Pu/Pije+ms1uPnv06P3790firY7Gk8tHl5dnR3fTwQGCMEfTJwfVjc/g5Rae9J4WhxPPw4/++tXz8uUP89F01h+dZweIS7jN//z73z1+n48G4/fofT6YXYFgD9MDdJXll1cgqhv4B+gRP+oGMnKTnc/yd9kUnlv7ZyF6dn1zUBzWH/HHf1feQkOp5wAN8nf5IJs8OfCOAtzt+TTwKPa7PUp7B2g8ybPRrDoWV+/5SLza43d59r58WX6reEc46F0+zc+GGbz75BYk5aOLCaTzycFFfziFf09n98PsrD+Rd8yjAYnT/Cc4NCDhASozwLV7Hf5/AP8zzyujqL0lO0Cz8XhYvKSHfvkFEY94qMOvcHlF4CoIyoe88j6PllekvGLllV8ew8qns/JQVh7DymMYXUchFgopL6GpQlJ7y+olPySrxNdklfj698TBijctdZvoxL43f094q+K/4n/lHekqmQ/fsfz3em8YMCcSHz8S8+RxNU7R9IofW42eWXY95SOX9pDf4wMQIx9GaRDCePMR7sFVSBCMS4R9xHz4J+6igF+HiIbwAEMUdRE/DlNUDFO/CxcsLF4sQD68GL83hNmBMLwRQz5FuBjdDMGYRsUMgdlCKBzh+8iHJ/G3x4S/BA0QC+BftIsYxMgnR4jhQApPhH/D2xNEMaL8yThEJEABfz3M+KQLujx0eEmCAg8FmL8gzC+YW+W8guO7iHI1QZWufHRzO1tI0fn1QNycjW9kLeBoaEbzllc2p4WO+LvHw/5ZNgSXeMUridC7/pDPiOKNLsajGRJFJOV9l5P+zVV+Pn2VzWbwrCn6e/9d/3l/lt2dwtFT8d7Fsefj0fTFZDyLxsPb69EUofPx0JMxj4e4dpvIqOEftPYAqz/g1x4IardD7fuO4RF0O83g/ceTqTi8Pxg840fMWwNk8pvR8P5kkvXf3ozzRRmPHxWG8zi7PR/mg7w/egODlb8LzwsS/lM0ZGE/IfZEIOPJ4NX9FEYwuvshm4yhx3jhEfZ7AWXdXtfzvRDm2H35UOCHR90eC0LKwpCA00Bo530+94Kjrh/4hAQ+PNjzAmgE9/qH/KB85+ydLFD/LpPaLyd8Xle6+T+eTU/Gw/ldhfqofzO7nRQLBwhhwjUdjy6HWTFCimYLrnz+9mx896ocGrR8rdf3N/CvSvrZZZF1NOFtFVr5ZXV9Vl4Xx/DI5FFecYxXHOGJsZYP5OO4R4ojiuuz8ro4CgZvGVqlFAuZogr9u3xa9DPvYGHWFCP/ycHdAbod5bPn5b9gBuXnbyupuHzC17fXZ9lkcWzLF8XaF73/gBd9/OjBGHs8vYEhOZheZdlMO+oKk1RGHTzpIsqGw1f1Q3vB/EhSZa728uUUFVmqnhN6q47DhscRw+Oo4XHM8Djf8LjA8LjQ8Liu4XE90zwbF8S0Iti0JNi0Jti0KNi0Kti0LNi0Lti0MNi0MsS0MsR4rphWhphWhphWhmgqkw35QmE8Qujq1flkPBwW3eFd7fZ58QLFzUmxaq56cv9+fMvXDtDoTuFM83bYP6ktEvndadGjq1Uk/Ptp+aoPD3tTu3t+8Am82TSbvIATreHC4aWgp6AvW3ydl/AOxb1I3t0fDsfvX8FaKO8Pk0E+G08WH3oNi9HX+Y00z+wft/DoS7jKJ5mI/WFGq8gQGmQX/dvhbMlhvD+fFqfgqDoV/6oPCzev43X68P9ZB+POeeeQUt+nPfoZnd/v1e7vXHTIZ2TFY3jFY2z+GHv4mD9/zH/wWOlUijM9fptNoBjV8gtWHrfj22m5mqy55gCSfQ3/LB+obKjPFxffgVuW9w6yy0kmXHZYfIRQ2nvx6MLKSrm7eKnTyfj62ejda1i5PAjg8SMR5ePp+SS/4QskdAanLG+z+RpokE/7cMYzqD+PrxehjuVkmOUz7uMxVPl4eDme5LOra64VHoIl5DQbXfWv0cU//3uCvpxkeTGcbmdXfHRdH10ewRvAahnWBMWHGOPJ2yKJr7O7Geqfjd/BI+Wz0Nt//tdolI3gyRfoZR/WkGf5cDA9v8on13Dv6HaCRv/8z6tscguLvPfFM2BtfpHDEfAOk8sMnjEcztD7bDLIRvC2sBLhMzTOM/RskGWfoe/h6ZC/AdzxIr/Lhp3i5gDWqh//43Y8+/x9/2qSjcrb6E02GfJIBtkUvS0ChJXlNQ/h/AreaYTejq8hrqOP/4Dp53DhfR7D2idHcOj51ewM8cNvpx2U5VzTMdyXDYvXQT/dostslE3yDN7tCMXw8EsIHsEbZoMcHoKHYeEyymYZenWTZ5fZECRzSbwy0KLgbWdoViw+R7fX8ELnchk2KbIMg+C2Gie+fySaGzQFND77O3S4B2u3+YSFh5esT6FD3Fz1+YdC844H46E+FotX+2o8qN65Om465J8moeu8PEO+7t/BCoS/3tkUWtcsg3aXZaP5B2plZPJTLo9/XAdPIT1+4577ZMhvXUAB50MYBlv+E8zC/oKa+UJ5Bmdwb0fZdFqszmbVur248TQfwHCR4fZHMF+LUQ9FvikXrzdZVi7/5BNvQH1xvlBfy5aFKSbP9XV/NECj4nODV9A/M/5Z3vxUtg8nhXfoCfo7pAHOCfkVnA4ecrVgSn1aCuc3mQwM7EU89VX5htXbKGNimE9nsravDlbXvtar6sUnHitPYfj1WXUth4BnOAQe2uoxd5lsoHRJbaHw6kIVZ27Fir9+Bl/eO2+Th/iDinMPxcnL4uSWxfneojjf/39xFouT3YHNTvlH+iIFL37kH+zfwUz8xOugyafifYvXKj/xWUxw9UDt6R+U42XdzzS7tGbbU97AvKp/FQ0Z/VT+ycIiWVVmz/s3RXcq7vsI5H3UnMNjXKWwtLa78krjJjMw5YPas5TMic8810ld/YOShwOZf2BSHS8/NDEbyKszcLKYgXuzDJxsKQObUBQtKhqYKYp2WFH8QNGP2ExT3KomcI3p8/7r7K/lffPFR/FZMpwY5Rfz07Li00Ov+iOCUVKSh0khZklJdrjQx6TSdPcJ9K9PdU384bIWnvJgXSsjsliy9m/v8mHen9wv1qqhdYho742jPVGina/CNxzuyjii5Vnb3MCwPB340PX1B1YvFtWLCPoTIuiP6JjfwCZljJX0YVeDLhFhxwQdFmGfGIedKGHD2rW7ncgXF9PPLh4soyHXHw/hXJrPIb6Wrk6zs3yWTao+Viyuy9vJaJDNu9vCovqUrF5VL/S+U7Irva8hPacE/c+//wfSZgUX2StKzjN0TJScHNPVOVF6KF1rOHubGhRw4v9JTD4tRwb/R0I+LQUXw4Twaxj06plV2jAIHgpOnbXh9eqcStmK5BPLGp8oNW5J8vIix5XaRFUbWaqN1hvR6zTomApfocJXqLGvKGEzZ74iwo6p8BXjsBMlbPCVba1rlMhP6cJCuPqQ9o/o2cW/QOZLl6EdzRwT983d5V/hafVX0YlfNBS6J4ZSzDpan3VUtFZa9Riqb62WMy/dlT5zSldbKK1ZKFUtlFlaKHsom7RioQ2qU1ls1VAsFZ8oits0FO3Qjiu1iao2slQbKWqddeaYCUNhwlCYsaEoYfecGYoIO2bCUIzDTpSwD8u/97gxFKY3FI2/sMpf2If5i7XdsH2yG1afk0zYDas6ENPbjeW8THelC52y1XbDanbDVLvxLe3GfyibtmM3q1Wnstiq3VgqPlEUt2k32qEdV2oTVW1kqTZS1Drr27Ev7MYXduMb240SNg6c+Y2IO/aF3xjHnShxH/asJtRaduMb241f2Y3vyG78fbIbvz4nfWE3ftWBfL3dWM7LdFe60Km/2m78mt34qt0ElnYTrLX63ZzdrFadymKrdmOp+ERR3KbdaId2XKlNVLWRpdpIUeuub8eB8JtA+E1g7DdK3MTZx06JiDsOhN8Yx50ocR92nZ1PngbGfhNUfhM48ptgn/wmqE/KQPhNULWgQO83lhMz3ZU2dBqs9pug5jeB6jehpd+Eiux2/Ga16lQWW/UbS8UnquIW/UY7tONKbaKqjSzVRopad307DoXfhMJvQmO/UeKm7s5vRNxxKPzGOO5EifswdHd+Exr7TVj5TejIb8J98puwPilD4Tdh1YJCvd9YTsx0V9rQabjab8Ka34Sq33Qt/ab7ULbVtN6c36xWncpiq35jqfhEUdym32iHdlypTVS1kaXaSFHrrm/HXeE3XeE3XWO/UeJm7v5+I+KOu8JvjONOlLgPA3d/vuka+0238puuI7/p7pPfdOuTsiv8plu1oK7ebywnZrorbei0u9pvujW/6ap+07P0m95D2WE7frNadSqLrfqNpeITRXGbfqMd2nGlNlHVRpZqI0Wtu74d94Tf9ITf9Iz9Rok7cPcFNBF33BN+Yxx3osR9yNx9/6xn7De9ym96jvymt09+06tPyp7wm17Vgnp6v7GcmKnahrY0wJs6b2+13/RqftNT/QZ7loaDvYfCrb73vznHWa07leVWHcdW84mquaViLx/ecaU3UfVGtnojVa/DLhhzNk/pO9gTxlPcMnMeTfBkS1tTdHvpRPAQh3Af8+ATTfCYujMgGX2zA4Go0oKw58iDsGab9e6aEPbq0xR7woZ4iovGVIwPjRHZztZ0Z7oTVGi1F4mJUJiRIKstuBG2dSO81tebNudGDdLTWtk1hmQp+0SV3aYhLRnqsdCcaDRHtpojVbPDvh5jLE0JS1PC5qakBu/u8zcZO4QhPck49kQTO3b3rY5TGb2BJ2HhSdiVJ+3MHnijiYoXJiqWnoRFc8JLPMlysqY706CgQg2ehOuepGo/xpZbQvkTHmjHVh9Zb9CUVmtPa3XXmJKl7hNVd6umpB/rsdCcaDRHtpojVbO7vh5jCR7AkjyAzdEDmnFqtdVsPU+S9AEs8QPmsSe6vDs8TSLmliTwBJi4sqR9QROU03RhAzeW2/Sx2LCOl2zUt52q6c60J6hQgyXVoQxYQ2XAtlgGrO5ibwfM0KQ9rdVdY0m2qAJVd6uWpB/rsdCcaDRHtpojTa2dtfUYS2YBltACbE4tUGN39+FXImOHMKQlmaML1NgPQ2eJP8VL2AU6SxIsA/yBMAN7S9oruAFe2AKOJd4Aiy3veAngwHaqpjvTnqBCDZZUhxxgDeUA22IOsLLf1q5NbdCSGkgHtbprLMkWdqDqbtWS9GM9FpoTjebIVnOkanbX1mMsqQdYYg+wOfdAjd3dF9ASGTuEIS3JHH6gxn7IrL4ftJ4lmdMPsMAfYFf8A7xXAAS8sE0cSwQCFtvi8RIIgu1UTTXtaUvf729syw0cBFwHIWANCQHbohCwuum8JRhCg/a0VneNJdkCEVTdLdV81ViPheZEozmy1Rypmh22xhhLNAKWbARsDkfQBE8cmpLkI2AJSDAPPtEEj91t2jrF5pAELCgJ2BUmAe8VJwEv7CbHkpSAxe55vISVYDtb053pUFChBleq8xKwBpiAbYkJWN1S3xIzoUF7Wqu7xpVsuQmq7lZdST/WY6E50WiObDVHqmaHjT3GEqCAJUEBmyMU1OAdfsVBMhSwhCiYh55o8t5z+A0Hc44CFiAF7IqkgPcKpYAXNpxjCVPAYoM9XoJTsJ2q6c60J6hQgyXVkQpYw1TAtlAFrGzuxS1hFRq0p7W6ayzJFq2g6m7VkvRjPRaaE43myFZzpGp2+AUHSVjAErGAzRkLaujM4VmSpCxgiVkwjz1RYz8MHJ4kmZMWsEAtYFesBbxXsAW8sCUdS9wCFlvw8RLggu1MTXemO0GFGhypDl3AGuoCtsUuYGX7r903VDfoSA3khVrdNY5kC19QdbfqSPqxHgvNiUZzZKs5UjW7a+sxlhAGLCkM2BzDoMbuDp+TyNghDGlJ5igGNfZD6vALDuYwBixoDNgVjgHvFY8BL+xax5LIgMUufbyEyWA7VVNNe9rSiGlsyw1YBlznMmANmAHbkhmwskMYt8RmaNCe1uqusSRbPoOqu6WarxrrsdCcaDRHtpojVbPD1hhjCWrAktSAzVENavAOLUmyGrCENZiHnmjy7vLnHbA5sAELYgN2hWzAe8VswAu72rGkNmCxjx8v4TbYztV0Z/oTVKjBk+rsBqyBNxBbeANRtgrjlugNDdrTWt1VT7LVfaLqbtWT9GM9FpoTjebIVnOkanbW1mN4b/GTqBLhQMwRDmroDj+4k7FDGPKHUc0JDmrsh4E7QqoMvtmRiAA4EFcAB7JXAAeysKudSIADT3H5U5pLAA62MzXdme4EFWr4tdg6wIFoAA7EFuBAlI3CuCWCQ4P2tFZ3jSPZEhxU3W060pKxHgvNiUZzZKs5UjU7/OCOSIADkQAHYg5wUGMP3X27QcYOYUhLMgc4qLEfEnc/EiGDN7AkwW8grvgNZK/4DWRhTzuR/AYi9vGTJfwG26maatrTln73uLEtN/AbSJ3fQDT8BmLLbyDKRmG772Bt0JIa+A21umssyZbfoOpuqearxnosNCcazZGt5kjV7LA1xkQCHIgEOBBzgIMavN0nzOt5kgQ4EAlwMI890STe4Q8XEXOAAxEAB+IK4ED2CuBAFja1EwlwIGIjP1kCcLCdq+nO9CeoUIMn1QEORANwILYAB6LsFCYtARwatKe1ums8yRbgoOpu1ZP0Yz0WmhON5shWc6RqdtfWYyIBDkQCHIg5wEGN3eFuWRk7hCEtyRzgoMZ+yLY02HSWZA5wIALgQFwBHMheARzIwqZ2IgEORGzkJ0sADrZTNdW0py0N98a23ABwIHWAA9EAHIgtwIEoO4VJSwCHBu1pre4aS7IFOKi6W6r5qrEeC82JRnNkqzlSNTtsjTGRBAciCQ7EnOCgBu/upyhk6BCFtCRzgIMm7w4xd8Qc4EAEwIG4AjiQvQI4kIVN7UQCHIjYyE+WABxsp2q6M+0JKtRgSXWAA9EAHIgtwIEo24RJSwCHBu1pre4aS7IFOKi6W7Uk/ViPheZEozmy1Rypmh1+bifxDUTiG4g5vkFTLmdmmsjYIQzpSOb0BjX2Q+aMwn5KzOENRMAbiCt4A9kreANZ2NBOJLyBiE38ZAm8wXamppqZuqU/nTZ25QZ4A6nDG4gG3kBs4Q1E2SVs9+eFDTpSA7yhVneNI9nCG1TdLdV81ViPheZEozmy1Rypmh22xphIeAOR8AZiDm9Qg3doSRLeQCS8wTz0RJN3h/AGYg5vIALeQFzBG8hewRvIwoZ2IuENRGziJ0vgDbZTNd2Z9gQVarCkOryBaOANxBbeQJRtwnb0rQ1aUgO8oVZ3jSXZwhtU3a1akn6sx0JzotEc2WqOVM0OP7WT8AYi4Q3EHN6ghr6tL0jqHEnCG4iEN5jHnqixu/wVWWIGb9AZlGA5kM2wHOz9aq/QDmRhuzuRaAcitviTJWgH23mcanrXllaWjT27Ae1A6mgHokE7EFu0A1H2EJOW0A4N2tNa3TV+ZYt2UHW3VPNVYz0WmhON5shWc6RqdvnDs0SyHYhkOxBztoMavLufnZWhQxTSsMzRDpq8d92BwokZ2kFnWIL0QDZDerA3rL0CP5CFzfBEgh+IAACQJeAH24mc7kzzggo1GFYd/EA04AdiC34gygZj0hL4oUF7Wqu7xrBswQ+q7lYNSz/WY6E50WiObDVHqmaHn/hJ7AOR2Adijn1QQ3e3TzWRsUMY0q/MuQ9q7C5RRMQM+6DzK0GBIJuhQNj71V5BIcjCRnkioRBEwAHIEiiE7TxONb1rS+ufxp7dAIUgdSgE0UAhqC0Ugirbj+1+V3uDftUAhajVXfUrW90nqu6War5qrMdCc6LRHNlqjlTNLkFF8O6VY1GJhaDmWAjNQHX364AydghDOJZ57Ikm8YG7703I4K0cS2NgVEAj6GagEev6Gd0rpARd2GZPJVKCl6foa3QJUsJ2nqc709ugQqv9jNaRElSDlKC2SAmq7F0mLSElGrSntbpr/MwWKaHqbtPPloz1WGhONJojW82RptbuPi+kEilBJVKCmiMl1Njd7YBNZOwQhrQzc6SEGru7370/lbGv7WaCN0E3w5tY2832ikZBF3boU0mjoIJKQJfQKGxnearpbFv6gk9jR2+gUdA6jYJqaBTUlkZBlV3PtCUaRYP2tFZ3jZvZ0ihU3S3VfNVYj4XmRKM5stUcqZrdddWYShgFlTAKag6jUGN3+H0NGTuEId3MHEahyTt1aGdmMAoDOxOoCroZVMXadrZXIAu6sLmfSpAFFUADugRkYTvNU01r29KitbGlN4AsaB1kQTUgC2oLsqDKjmnaEsiiQXtaq7vGzmxBFqrulmq+aqzHQnOi0RzZao5UzQ7bakwlyYJKkgU1J1mowbsDQyUydghD+pk5yUKTeIc/HkXNSBYGfiY4F3QznIu1/WyvKBh0gQxAJQWDChoCXULBsJ3n6c70NqhQg5/VKRhUQ8GgthQMqmy3tvt7ygb9rIGCUau7xs9sKRiq7lb9TD/WY6E50WiObDVHqmaHrEAqIRhUQjCoOQRDjb3rjl8rY4cwpJ2ZUzDU2N39xAc1Y2AYmJkgZNDNEDLWNrO94mfQBaYAlfwMKjgKdAk/w3aSp5rGtqVJ3tjQG/gZtM7PoBp+BrXlZ1BlpzZtiZ/RoD2t1V1jZrb8DFV3SzVfNdZjoTnRaI5sNUeqZncsdir5GVTyM6g5P0MNPXDHvZWxQxjSy8z5GWrsh3Z06fXczIyfYW9uArZBNwPb2LTX7RWZgy7QCqgkc1BBaKBLyBy2PSDV9L2WfjGYNpA5aJ3MQTVkDmpL5qDKFnDaEpmjQXtaq7vG62zJHKrulmq+aqzHQnOi0RzZao5UzQ6bbkwlmYNKMgc1J3NoCubwzE2iOahEc5jHnmgST92hOagZmsPe7QTHg26G47Fpt9sr6AddACFQCf2gAv5Al0A/bLtAqplILf3MFm2AftA69INqoB/UFvpBlQ3ktCXoR4P2tFZ3jdvZQj9U3S3VfNVYj4XmRKM5stUcqZodNt2YSuwHldgPao79WHegrud2EvtBJfbDPPZEk3iHbET6QdgPA7cTUBC6FSjI2m63V8gQuoBRoBIZQgU6gi5Bhth2gXRnOh9UqMHt6sgQqkGGUFtkCFV2n9s1wA26XQMypFZ3jdvZIkNU3a26nX6sx0JzotEc2WqONLV2uANAEkOoJIZQc2KIGjv23DFDZPAQh3Q7c2aIGry7rRen9IOQIQZmJ4AidCtAkbXNbq9wI3QBwUAlboQK7ARdghuxbQKppvG19NNgtAE3Quu4EarBjVBb3AhVtq7TlnAjDdrTWt01ZmeLG1F1t1TzVWM9FpoTjebIVnOkana53U3yRqjkjVBz3ogaO/bc/TaYDB7ikGZnDhzRBO9wg8AH8UbsvU/ASehW4CSbtsK9IpnQBboDlSQTKogWdAnJxLZFpJq22NLvv9AGkgmtk0yohmTCbEkmTNn1TlsimTRoT2t1V63QVveJqrulmq8a67HQnGg0R7aaI1Wzu44cw5tXVsgkyISZg0zU2N0B6xMZO4QhnNA89kSTd3ekSBn7dp2QCcoJc0E5WdcJ2V4xUNgCF4JJBgovbdER2RIGim2HSDVu0BLknzUwUFidgcI0DBRmy0Bhyo55O+2bc8IG7Wmt7hontGWgrKt7s064ZKzHQnOi0RzZao5UzQ5/L5pJBgqTDBRmzkBRY3fphJKBwiQDxTz2RJN3d+eEMvYtO6EgpDAXhJS1nXCv+ClsgSnBJD+FCY4GW8JPse0QqaYrtkRjZg38FFbnpzANP4XZ8lOYyk9pywkb+Cm1umuc0Jafsq7uDTuhfqzHQnOi0RzZao5UzS7PCSU/hUl+CjPnp6ix99z9KVDGDmFIJzTnp6ixE2e/M3TKNoFPMXBCAVdhLuAqazvhXqFX2AKOgkn0ChMIDrYEvWLbIVJNV2zLCRvQK6yOXmEa9AqzRa8wFb3SlhM2oFdqddc4oS16ZV3dG3ZC/ViPheZEozmy1Rypmt115JhJ8gqT5BVmTl5RY3f5h0IZPMQhrdAcvaJJvLNfVThlmyCvGFih4LIwF1yWta1wr6gtbIFkwSS1hQl6B1tCbbFtEammLbZlhQ3UFlantjANtYXZUluYSm1pywobqC21umus0Jbasq7uDVuhfqzHQnOi0RzZao5Uze46cswktYVJagszp7aosWPPHVVTBg9xSCs0x7ZoEu/uC6JsE9wWe2cUkBfmAvKyaaPcKyIMW6BkMEmEYYIMwpYQYWwbSKppmm0ZZQMRhtWJMExDhGG2RBimEmHaMsoGIkyt7hqjtCXCrKt7w0apH+ux0JxoNEe2miNVs8MvlzKJhGESCcPMkTBq7Nhzh+uUwUMc0ijNmTCaxDv8Ss0WkDAGRimAMawFYMzaRrlXOBm2gNhgEifDBFaELcHJ2DaQVNM02zLKBpwMq+NkmAYnw2xxMkzFybRllA04mVrdNUZpi5NZV/eGjVI/1mOhOdFojmw1R6pmd/06ZpImwyRNhpnTZNTYsefwGzcSJ8MkTsY8+ESTeIffuNkCTcbAKAVrhrXAmlnbKPeKRMMW6BxMkmiYIJKwJSQa2waSapqms7/1H1ej+JNj0kEn/M9PZZA343w005W0ekA+vaGiIopFJQErpPCrs/Lqw2r6O6jkeDKYorvyqej+yYHPz1LQT9DJxGsVIb/KfxLJrd87ux8uGyRqsk5ksigki9om60RNVpEeF6O/nim8ZqZwc6YimSkGmWK2mYp2JFNk+5mKZabg1OfEt81UvCOZotvPVCIzBd53EthmKtmRTLHtZ+pUZiqETIW2mTrdkUz5289UKjPVhUx1bTOV7kimgu1n6qnMVA8y1bPN1NMdyVS4/Uw9k5nCHqQKe7a5erYjueqKXLGt5eqLea4wzxW2zdUXO5Kr3vZz9eU8V3ytjq0X61/uSK6wt/1kPZ8ni6/VsfVi/fmuJAtvP1lfzZPFl+vYer3+1a4ki2w/WV/Pk8VX7Nh6yf71riRLrtnp1pL1zTxZfNGOrVft37hM1jcXF9NsxnNz6NMiNYfENJls+8l8MU8mX9dj64X9i10Zef72k/XtPFl8aY+t1/bftjTy+KdhxcijhskMtp/Ml/Nk8tU/tl7+v9yVkSfX/2RryXo9/0iVr/+J9fr/9a4kq7v9ZH03TxY/ASDWJwDf7UqyettP1pt5sopP663PAN7sSLKIPAPAW0vWD/Nk8TMAYn0G8MOuJAtvP1nHP+J5uvg5ALE+B+AvsSMJk2cB3tYSdlJPGD8PINbnASe7kzC6/YRF9YTxcwFifS4Q7U7CxGq/+O2dLf1hqJ4wvt4n1uv9eHcS5m8/YUk9YXzNT6zX/MnuJEys6oufjNjSn4nqCePremK9rj/dnYSF209YWksY5Wt7ar22T3cnYWJ1z8Lt/dGonjC+vqfW6/unu5Ow3vYT9qyeML7Gp9Zr/Gc7kzAqVvks2N4fkOoJK76VY73O/2J3EiZW+mx7f538sp4wvtKn1iv9L3cnYWT7CXteTxhf6VPrlf7z3UmYWOmzLf41qZ4wvtKn1iv9r3YnYXKlv71PV7+uJ4yv9Kn1Sv/r3UmYXOlv73Owb+oJ4yt9ar3S/2Z3EhZsP2Ev6gnjK31qvdJ/sTsJkyv97X0e9m0tYZz6fMKsV/rf7k7C5Ep/ex/vvKwnjK/0mfVK/+XuJEys9On2Pq14VU8YX+kz65X+q99Uwl7XE8ZX+sx6pf/6N5Ww7+oJK76Gb73S/+43lbA39YTxlT6zXum/+U0l7Pt6wvhKn1mv9L//TSXseT6dZSJnPx9Dxjoo6qC4g5IOOu2gtIOedtCzDvqig77soOcd9FUHfd1B33TQiw76toNedtDrDvqug9500A8ddPwjt1p+EfGLmF8k/OKUX6T84im/eMYvvuAXX/KL5/ziK37xNb/4hl+84Bff8ouX/OIVv3jNL77jF2/4BdTqV11Fh6Dq4IHENWqKvbWrOsxHWVmZ2VV+/nYEVXhyQMTQ9MobT/PBIBtVdTMt8qFa5Qe5GM1l9lsd2v1Rft2f8dEHFbnhOtH0JssGxS2ZiRt4uXx0uRDMfFIcik+kxFJ7HsUHpDj7x6h8ypRfPjmAaTDMz/NZ88Q5r+bM3b99Qj5Ff0L3xfUTNOHX4k3PxyO+rVIdoNUD8rXarMoH5S2/zEbvINLxZIrQnSe28Hnl+6OfxD13GEpWfuqKRc1wrZHBeJjkd+hYHH8sjjom/GfhvfLPdMe0et1jJm74NaUPqwiD6jy/gAQ3VvF08VcKLrLJLL/8S7V9WC3b4u7hLcH8zy7lkcQrt6UW12f8j5a+PJ7ftqhzw1IWhC2mIobXPB5ejif57Or6dorewcEn8KxsdNW/Rj/dTtDlpH+RT8+vshGK+xOY0cPh7ejy4z9g73N+8JeTLIejUf/2Ar3sw8OTs3w4gOPzCYRhluIyrDYnx8UYIptmk/xCFncKHbl4zWq0VVNiOutPZi94c0ZFnyK9o7DrEdIjAfGxT8Py+7s9ctQNvC7uhiHDOORU3bmxNxdpkSX+Ebr70XvifWSeTQ1222E28+nz/uvsr+V9843Y9SSX0TzMsafNMTkKPNzzfcKCbsBC1itT3A2PetTzeiTsQQVwGNilmD5I8T2keIIscqzhue5zjrs9GrAu6fm9oMd6QVjmmB1h2vW6FPs9xjyP2uWYPcjxgA9jmxxrUID7nWPMgrAX0AAcj+Ayxd5Rl3Thvi5jftC1Hca+kuKfcWeU3f76BG71h7Nf/0TuqhvYJvMattQeZx4f+QGB4ctoNwgpJYHoIKwHBksJYZixwHJ0B2rqiUx9WYRDci+S/6tN9jXAkv3NPguPCPV6PRz6PZgB2GMi+zDoaa8Xsm7QCz1sl/1QzX6R+78Ns4vZ337+28Wkf/6zLEQHQcqGU/SLvOcXzlj5Rdbsl19/lrc7aDoeTWdWFQv/L1UM5kvghV3Wg7ZEiF95ATmivke7PoEa+pz5aFOurrKiKcv1Qc2p+38p2QzSSjCmPvSgHiWU+kW6Q3yEfVg9EljxkNDaFxZ/qxvx9Y1mflTdyWR2VIce4vnsQOYV0/xK9v5WjHhHsOQMcEiZx3gPKwtGjyiDeQEuQ/yA0dCuYNhbqNjx2dnk9vzqLBvko0s44foMfXSHPr6EUt5bTBSs+U3W3cr7krOtZVOFeAEJwCtgjep1A1IkPmBHIRSi59MeBTOhS2380TkfuJBW/uEU//dlNr7Mzib9P/8vUEsHCF5+KTdgJwAAY5UBAFBLAQIUABQACAAIAFhCYUHWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAWEJhQV5+KTdgJwAAY5UBAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAD3JwAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | ||
| + | [[Kategorie:Linalg]] | ||
|} | |} | ||
</div> | </div> | ||
Aktuelle Version vom 1. November 2012, 09:19 Uhr
Aufgaben zum Einstieg
Aufgabe 1Lassen Sie die folgenden Punktmengen in der obigen Geogebraapplikation grafisch darstellen. Um was für geometrische Objekte handelt es ich in jedem Fall? Begründen Sie Ihre Antwort. Aufgabe 2Lassen Sie die folgenden Kreise mittels Geoegebra grafisch darstellen, indem Sie jeweils eine entsprechende Gleichung in die Eingabezeile eintragen.
Kreise in der synthetischen GeometrieVereinbarungAlle unsere folgenden Betrachtungen beziehen sich auf die Geometrie in der Ebene. KreisdefinitionDefinition Es seien Abstände von Punkten
Analytische Beschreibung von Kreisen mittels des Satzes von PythagorasKreis in Mittelpunktslage
allgemeine LageDerAlgorithmus von Bresenham
|
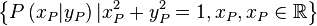
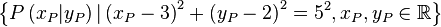
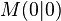 Radius:
Radius: 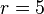
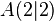 Radius:
Radius: 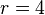
 ein Punkt und
ein Punkt und  eine positive reelle Zahl. Unter dem Kreis mit dem Mittelpunkt
eine positive reelle Zahl. Unter dem Kreis mit dem Mittelpunkt 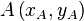 und
und 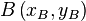 .
. ist der Schnittpunkt der Senkrechten durch
ist der Schnittpunkt der Senkrechten durch  auf die x-Achse mit der Senkrechten von
auf die x-Achse mit der Senkrechten von  auf die y-Achse.
auf die y-Achse.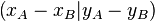 .
.
 ist rechtwinklig. Nach dem Satz des Pythagoras gilt:
ist rechtwinklig. Nach dem Satz des Pythagoras gilt: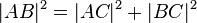
 schreibt sich (I) wie folgt:
schreibt sich (I) wie folgt: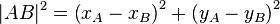
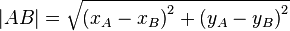
 in Mittelpunktslage, Radius:r
in Mittelpunktslage, Radius:r
