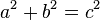Lösung Aufgabe 2.2 WS 12 13: Unterschied zwischen den Versionen

Aufgabe 2.2

Der Satz des Pythagoras lautet:
Im rechtwinkligen Dreieck ist die Summer der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse.

(a) Formulieren Sie den Satz des Pythagoras in Wenn-Dann.
(b) Formulieren Sie die Umkehrung des Satzes von Pythagoras.
(c) Formulieren Sie die Kontraposition des Satzes von Pythagoras.
(d) Auch die Umkehrung des Satzes von Pythagoras ist wahr. Formulieren Sie ein Kriterium dafür, dass ein Dreieck rechtwinklig ist.
(e) Definieren Sie den Begriff des rechtwinkligen Dreiecks mittels des Kriteriums aus Teilaufgabe (d).

Lösung von User: Yellow

a) Wenn ABC einen rechten Winkel hat, dann ist die Summer der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse.
b) Wenn die Summer der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse, dann ist das Dreieck ABC ein rechtwinkliges.
c) Wenn die Summer der Quadrate der Kathetenlängen ungleich dem Quadrat der Länge der Hypotenuse, dann ist das Dreieck ABC kein rechtwinkliges.
d) Wenn ABC einen rechten Winkel hat, genau dann ist die Summer der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse.
--Yellow 12:44, 6. Nov. 2012 (CET)

Lösung von User: B.....

a: Wenn in einem Dreieck die Summe der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse ist,
dann ist es ein rechtwickliges Dreieck.

b: Wenn das Dreieck rechtwicklig ist,
dann ist die Summe der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse.

c: Wenn das Dreieck nicht rechtwinklig ist,
dann ist die Summe der Quadrate der Kathetenlängen nicht gleich dem Quadrat der Länge der Hypotenuse.

d: Genau dann,
wenn die Summ der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse ist,
ist das Dreieck rechtwinklig.

e: Ein Dreieck ist rechtwinklig,
wenn die Summe der Quadrate der Kathetenlängen gleich dem Quadrat der Länge der Hypotenuse ist.
--B..... 22:33, 6. Nov. 2012 (CET)

Lösung von User: Caro44

(e) Definition rechtwinkliges Dreieck

Ein Dreieck ist genau dann rechtwinklig, wenn das Quadrat der gegenüberliegenden Seite des rechten Winkels gleich der Summe der Quadrate der beiden anderen Seiten ist.

ODER

Ein Dreieck ist genau dann rechtwinklig, wenn das Quadrat der längsten Seite des Dreiecks gleich der Summe der Quadrate der beiden anderen Seiten ist.--Caro44 13:52, 7. Nov. 2012 (CET)

Bemerkungen m.g.

a)

@yellow: Prinzipiell richtig, reine Syntax: \overline{ABC} generiert und verdeutlicht somit, dass es sich explizit um ein Dreieck handeln soll.
--*m.g.* 23:11, 6. Nov. 2012 (CET)
@B.....: Wenn Yellows Formulierung prinzipiell richtig ist, dann kann es Ihre nicht sein. Kann man eigentlich bei einem beliebigen Dreieck von Katheten und der Hypotenuse sprechen?--*m.g.* 23:11, 6. Nov. 2012 (CET)
weiter @B.....: Sie haben eine neunte Klasse und müssen den Satz des Pythagoras behandeln. Sie wollen, dass die Schüler den Satz selbst entdecken. Didaktisch geschult wissen Sie, dass der Beweis des Satzes zunächst nicht die Hauptrolle spielt. Sie möchten, dass Ihre Schüler den Satz selbst entdecken. Diesbezüglich entscheiden Sie sich für die sogenannte induktive Satzfindung. Welcher Arbeitsauftrag führt zum Satz des Pythagoras und welcher zur Umkehrung des Satzes von Pythagoras:

1. Sie lassen jeden Schüler ein rechtwinkliges Dreieck zeichnen. Die Schüler sollen dann die Länge der Seiten messen und die Quadrate der Seitenlängen berechnen. Danach vergleichen die Schüler die Summe der Kathetenquadrate mit dem Hypotenusenquadrat. Voraussetzung: rechtwinkliges Dreieck, Behauptung:
2. Sie geben den Schülern Dreiecke vor, deren Seitenlängen Pythagoreische Zahlentripel sind. Die Schüler stellen fest, dass es sich in jedem Fall um ein rechtwinkliges Dreieck handelt. Voraussetzung: , Behauptung: rechtwinkliges Dreieck.--*m.g.* 23:26, 6. Nov. 2012 (CET)

e)

@B.....: Wir legen fest, was ein rechtwinkliges Dreieck ist. Erst wenn man weiß, was ein rechtwinkliges Dreieck ist, kann man sich überlegen, was Katheten sind und was eine Hypotenuse ist. Ich kann also in der Festlegung des Begriffs rechtwinkliges Dreieck noch nicht die Begriffe Kathete und Hypotenuse verwenden.--*m.g.* 23:32, 6. Nov. 2012 (CET)