Lösung von Zusatzaufgabe 3.1P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
Geben Sie eine exakte Realdefinition des Begriffs ''Winkelhalbierende'' an (orientieren Sie sich gegebenenfalls an Schulbuchdefinitionen). Notieren Sie, welche anderen Begriffe Sie dazu verwenden.<br /> | Geben Sie eine exakte Realdefinition des Begriffs ''Winkelhalbierende'' an (orientieren Sie sich gegebenenfalls an Schulbuchdefinitionen). Notieren Sie, welche anderen Begriffe Sie dazu verwenden.<br /> | ||
| − | + | *Eine Winkelhalbierende ist eine Halbgerade, die durch den Scheitelpunkt eines Winkels läuft und diesen in zwei gleichgroße Winkel teilt. Andere Begriffe: Halbgerade, Scheitelpunkt --[[Benutzer:Der Bohrer|Der Bohrer]] 11:48, 30. Nov. 2012 (CET) | |
| + | **Gut. Das ist eine Möglichkeit, allerdings noch nicht ganz exakt. Wichtig ist bei den meisten zu defninierenden Wörtern, dass sie im Bezug auf etwas definiert werden müssen. <br /><ggb_applet width="484" height="268" version="4.0" ggbBase64="UEsDBBQACAAIALptfkEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIALptfkEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vrrcts2Fv6dPgWGv2MKN4JkRkonzm0zkzadOrvt7D+IhCTUFMklqVumL9U+SJ+pBwApkVLsOHbiiTursQwCOMDBOd+5gfb4++0yQ2tV1brIJx7xsYdUnhSpzucTb9XMziLv+6ffjeeqmKtpJdGsqJaymXjcUOp04iXBNIkEj86CNGBnHAfR2TQNkzMai2QWc07VTHoIbWv9JC9+lEtVlzJRF8lCLeXbIpGNZbxomvLJaLTZbPyOlV9U89F8PvW3deohOGZeT7z24QlsN1i0YZacYkxGv/7w1m1/pvO6kXmiPGREWOmn3z0ab3SeFhu00WmzmHgBBjEWSs8XRiYceGhkiEpQSKmSRq9VDUt7XStzsyw9SyZzM//IPaFsL46HUr3WqaomHva5h4pKq7xpJ0nLZNQtH6+12rh9zJNlAYuaosim0myBfv8dUUwxemwa4hoKjRBuCrsxzFxDXcNdEzga7pZzR8odDXc0nHlorWs9zdTEm8msBpXpfFYBXPt+3ewyZc/TDhzEJY9Bplp/AGJmFOp0DOMYPzZfAV9uJkZDIUmPa1OtPpNpx5JH/OYs6Z0EZR1P+jExaXCFmOIapk7um8hJgh5PYGV/7PeEI7tOzGOOrn83hoLfi4jjUecq49Y7UL0wtK31NGpZG39hMQpiY/YEBeAbIgQrDxCJoQkpAm9AJEA8gC6JkDBtiFgIExwxFCFDRxiyzhFE8IuHdjOBAtjMjIbgk4gAI44Choj1KY7Ak5D1S/BRyoAiCFAAiwx7Qs0WTCAuoMcixOGMxiVDAoQMFkIf2FPECGJmMQkRFUiY/Qg3ri4ic3TYkiKBkSBmQ/Bq8GjnzUAfIWakEa26dF6umoGKkmXaPTZFuccCqCEeHcKci0+DKPhonMmpyiAxXBgkEVrLzHiEZTQr8gZ1IFI3Nq9kudBJfaGaBlbV6De5lm9lo7avgLrueFvapMjrn6qieV5kq2VeI5QUGd6fuchI75nuTw0d1pvg/YmgNyF6z+FH+RYwg1a1Av5FVXfkMk3fGIpDaABNvsuz3Xml5GVZ6KEY45HNMWO1SjKdapn/B4zVcDF6QV3KseGqSzmU4+4gRZVe7GqwYLT9r6oKmCOBSbI712Om1/8AxnUijb/x2I8HH1jUTgV4uKiFS633oMitOsg3r4wz9zpv6vMiOwxZkZ/LsllVtkCAeFgZQZ7l80xZs7ARFrJvcjktthfOHpjb6/2uhF4r73RuVY0gHNAA0u68baeutTTmaHsqbGmwpcCdgel0P09iailsO3WtpQKLdUdrRSWdmAR3bHRtgxj2WlfpApSxd5PMV7lu3nadRieXrajELfhxtZyqvdUM9yRfas/x6MisxpeqylXWWjGAuSpWtXPKnoGnKtFL6LqJViXSwPVvOIAbTdW8Ut3BM1t8OYXZ2YGBngzbrV5VxfJNvn4PtnB0gPGoO+W4TipdGptDU4j8l+pgVamuJSSOtL/OuB2InpgEAeppjGrAIVfNoqhsfQVxBFrjbZlaQnGFGmte1kL3an5myzSjT1RMf4NQts92bv4AGEx/1NSsUcqsXEhTyrVCZ3KnqoEa7H4/FOmxckD3VgLw69JhWyrlzMKdFx5K2M560yAugbZrtJ14Z8Rn4Oo7cDY/hMjxwVXprkw1whonG8RiN3qEFJiP09MnNHb+D9AY9SEFGY3R+9DY83+AxpjPo05j4otoLCmWS5mnKLcVoM0P3qEikdj4JpLEGByS1GjRqWjVdPN//eH2bHc6QcFGnr2WgdrepGS2ao9EfYqDWJA4YBGN4rg9+e2AIrjLPAegyA2BOslDDVRFl3D1q22ybNq0aB/+pdNU2YrYgVslPdV3iGdZsflZzTK1tXp1s708cQUIP8vdEQTnDoJnJ7qX16u+gp06rclPmH/P4K6yf3x76x/ESWxNGHcmfMbBAqDA2n/I7YFQ/8vdktplab0sM53oZq+5zLjXm7yBnK1s0jpNxZdKlaYGepe/r2Remzcpd4bu1G2mN4du+q1AB2vJoIANTNzeueQXHNe2H0wqFFEPWHwHF7t3ZK/LJS8efi4hftBWK/irp96XD19d1Bf76u7LZN7rFPbq4SuM+XFbqQTRPVUqL1ysfekqlVenlcqfn1Wp/HlcqRA/wjiGLxWYkljw/1cqx+nupYPgxYnuk5unu+QbSXdQoAxzWtTlOiIGL2uItW/qMz4YDh9QsjtxrlUmq3NtNi+qz7wQpNdDbfSxxzI9xXr4AuYeaxu4e+AoDkO4iogowu5qCuOcwRinMMk5wSJyV1WYCLEwFxcRCcoDxvjXwftqmH6yOWMITnoCx+vr4Rgmnte3SjyEujeDtv3SyceExVtdlWkYYMwYCYXgosMz8AmhJMQRAch4QMlXyE1X3gJen4Dzi84vVbaQ2VSrSuWpOv8EXP1A+bHFd60bbu5M72azWjVW17z1Fc5v6GwQK8M+Cnh/jSDBADQHD4xHxgMZZoITEoPXPdjYemXOPK1XZjc3hdk3kjMBwHCQM0MLLPEpO06lBtcQKirSv1I+IFhH/Vff9o9K7T9EPP0bUEsHCNOhCKN9BwAArSEAAFBLAQIUABQACAAIALptfkHWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAum1+QdOhCKN9BwAArSEAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAUCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | ||
| + | Ist <math>BG^+</math> eine Winkelhalbierende des Winkels <math>\angle DEF ? Wie muss die Definition ergänzt werden?--~~~~ | ||
| + | </math> | ||
| + | |||
| + | |||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Version vom 30. November 2012, 13:48 Uhr
Geben Sie eine exakte Realdefinition des Begriffs Winkelhalbierende an (orientieren Sie sich gegebenenfalls an Schulbuchdefinitionen). Notieren Sie, welche anderen Begriffe Sie dazu verwenden.
- Eine Winkelhalbierende ist eine Halbgerade, die durch den Scheitelpunkt eines Winkels läuft und diesen in zwei gleichgroße Winkel teilt. Andere Begriffe: Halbgerade, Scheitelpunkt --Der Bohrer 11:48, 30. Nov. 2012 (CET)
- Gut. Das ist eine Möglichkeit, allerdings noch nicht ganz exakt. Wichtig ist bei den meisten zu defninierenden Wörtern, dass sie im Bezug auf etwas definiert werden müssen.
- Gut. Das ist eine Möglichkeit, allerdings noch nicht ganz exakt. Wichtig ist bei den meisten zu defninierenden Wörtern, dass sie im Bezug auf etwas definiert werden müssen.
Ist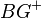 
eine Winkelhalbierende des Winkels Fehler beim Parsen(Lexikalischer Fehler): \angle DEF ? Wie muss die Definition ergänzt werden?--~~~~
