Serie 6 (WS 12 13): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgaben zum Abstand= ==Aufgabe 6.1== <u>'''Satz:'''</u> ::Es seien <math>A,B</math> und <math>C</math> drei paarweise verschiedene Punkte.<br /> ::Wenn der Pun…“) |
(→Aufgabe 6.2) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | =Aufgaben zum Abstand= | + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> |
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | |||
| + | =Aufgaben zum Abstand und zu Strecken= | ||
==Aufgabe 6.1== | ==Aufgabe 6.1== | ||
| Zeile 8: | Zeile 13: | ||
<br /> | <br /> | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe 6.1_S (WS_12_13)]] |
==Aufgabe 6.2== | ==Aufgabe 6.2== | ||
| Zeile 18: | Zeile 23: | ||
<br /><br /> | <br /><br /> | ||
| − | [[Lösung von Aufgabe 6. | + | [[Lösung von Aufgabe 6.2_S (WS_12_13)]] |
==Aufgabe 5.3== | ==Aufgabe 5.3== | ||
| Zeile 29: | Zeile 34: | ||
==Aufgabe 6.4== | ==Aufgabe 6.4== | ||
| − | + | Definieren Sie den Begriff Viereck. | |
| − | + | ||
<br /><br /> | <br /><br /> | ||
[[Lösung von Aufgabe 6.4_S (WS_12_13)]] | [[Lösung von Aufgabe 6.4_S (WS_12_13)]] | ||
| + | ==Aufgabe 6.5== | ||
| + | Definieren Sie den Begriff Diagonalen eines Vierecks. | ||
| + | |||
| + | [[Lösung von Aufgabe 6.5_S (WS_12_13)]] | ||
| + | |||
| + | |||
| + | ==Aufgabe 6.6== | ||
| + | Ein konvexes Viereck ist ein solches, dass keinen überstumpfen Innenwinkel hat. Das Problem ist, dass unser derzeitiger Aufbau der Geometrie eine solche Definition nicht zulässt, da der Begriff des Winkels noch nicht klar ist. Formulieren Sie trotzdem eine Definition des Begriffs "konvexes Viereck", die mit den uns bereits zur Verfügung stehenden Begriffen auskommt. | ||
| + | |||
| + | [[Lösung von Aufgabe 6.6_S (WS_12_13)]] | ||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 2. Dezember 2012, 14:52 Uhr
|
Aufgaben zum Abstand und zu StreckenAufgabe 6.1Satz:
Beweisen Sie diesen Satz.
Aufgabe 6.2Es seien
Aufgabe 5.3Zeigen Sie, dass für drei paarweise verschiedene Punkte
Aufgabe 6.4Definieren Sie den Begriff Viereck.
Aufgabe 6.5Definieren Sie den Begriff Diagonalen eines Vierecks. Lösung von Aufgabe 6.5_S (WS_12_13)
Aufgabe 6.6Ein konvexes Viereck ist ein solches, dass keinen überstumpfen Innenwinkel hat. Das Problem ist, dass unser derzeitiger Aufbau der Geometrie eine solche Definition nicht zulässt, da der Begriff des Winkels noch nicht klar ist. Formulieren Sie trotzdem eine Definition des Begriffs "konvexes Viereck", die mit den uns bereits zur Verfügung stehenden Begriffen auskommt. |
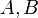 und
und  drei paarweise verschiedene Punkte.
drei paarweise verschiedene Punkte. zwischen den Punkten
zwischen den Punkten  und
und  vier paarweise verschiedene Punkte.
vier paarweise verschiedene Punkte.  und
und  gilt:
gilt: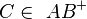 und
und 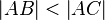 dann gilt
dann gilt 

