Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Restklassen modulo 4) |
*m.g.* (Diskussion | Beiträge) (→Restklassen modulo 4) |
||
| Zeile 26: | Zeile 26: | ||
*<math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}</math>.<br /> | *<math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}</math>.<br /> | ||
Kommutative Gruppen werden auch Abelsche Gruppen genannt. | Kommutative Gruppen werden auch Abelsche Gruppen genannt. | ||
| + | ==Gruppe der Deckabbildungen des Rechtecks== | ||
Version vom 9. Dezember 2012, 18:15 Uhr
Beispiele für endliche Gruppen
Restklassen modulo 4
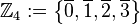
mit
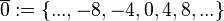 (Menge aller durch 4 teilbaren ganzen Zahlen),
(Menge aller durch 4 teilbaren ganzen Zahlen),
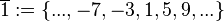 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
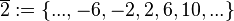 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
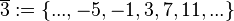 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),
Wir definieren auf  eine Verknüpfung
eine Verknüpfung  wie folgt:
wie folgt:
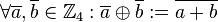
Die Struktur 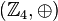 ist eine Gruppe:
ist eine Gruppe:
- Die Verknüpfung
 ist auf der Menge
ist auf der Menge  abgeschlossen, d.h.
abgeschlossen, d.h. 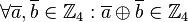 ,
,
- Die Verknüpfung
 ist auf der Menge
ist auf der Menge  assoziativ, d.h.
assoziativ, d.h. 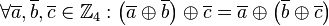 ,
,
 hat ein neutrales Element, nämlich die Klasse
hat ein neutrales Element, nämlich die Klasse  , d.h.
, d.h. 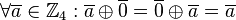 ,
,
- Zu jedem Element aus
 gibt es ein inverses Element, d.h.
gibt es ein inverses Element, d.h. 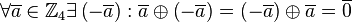 .
.
Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:
Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen.
Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe 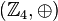 :
:
Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung  auf
auf  kommutativ ist:
kommutativ ist:
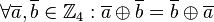 .
.
Kommutative Gruppen werden auch Abelsche Gruppen genannt.

