Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Restklassen modulo 4) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> | ||
| + | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- hier drüber nichts eintragen ---> | ||
| + | |||
| + | |||
=Beispiele für endliche Gruppen= | =Beispiele für endliche Gruppen= | ||
==Restklassen modulo 4== | ==Restklassen modulo 4== | ||
| Zeile 27: | Zeile 33: | ||
Kommutative Gruppen werden auch Abelsche Gruppen genannt. | Kommutative Gruppen werden auch Abelsche Gruppen genannt. | ||
==Gruppe der Deckabbildungen des Rechtecks== | ==Gruppe der Deckabbildungen des Rechtecks== | ||
| + | |||
| + | |||
| + | <!--- hier drunter nichts eintragen ---> | ||
| + | [[Kategorie:Linalg]] | ||
| + | |||
| + | |} | ||
| + | </div> | ||
Version vom 9. Dezember 2012, 18:17 Uhr
|
Beispiele für endliche GruppenRestklassen modulo 4
Wir definieren auf Die Struktur
Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:
Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen. Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe
Kommutative Gruppen werden auch Abelsche Gruppen genannt. Gruppe der Deckabbildungen des Rechtecks |
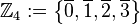
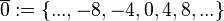 (Menge aller durch 4 teilbaren ganzen Zahlen),
(Menge aller durch 4 teilbaren ganzen Zahlen),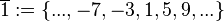 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),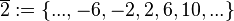 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),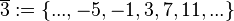 (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),
(Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen), eine Verknüpfung
eine Verknüpfung  wie folgt:
wie folgt: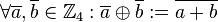
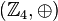 ist eine Gruppe:
ist eine Gruppe:
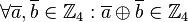 ,
,
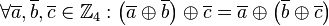 ,
,
 , d.h.
, d.h. 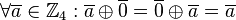 ,
,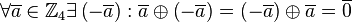 .
.
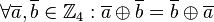 .
.
