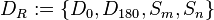Gruppen, abelsche Gruppen 2012 12: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Gruppe der Deckabbildungen des Rechtecks)
(→‎Beispiele für endliche Gruppen)
Zeile 31: Zeile 31:
 
Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung <math>\oplus</math> auf <math>\mathbb{Z}_4</math> kommutativ ist:<br />
 
Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung <math>\oplus</math> auf <math>\mathbb{Z}_4</math> kommutativ ist:<br />
 
*<math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}</math>.<br />
 
*<math>\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}</math>.<br />
−
Kommutative Gruppen werden auch Abelsche Gruppen genannt.
+
Kommutative Gruppen werden auch Abelsche Gruppen genannt.<br /><br />
 +
==Gruppe der Deckdrehungen des Quadrats==
 +
Hierbei verstehen wir unter <math>D_D</math> die Menge aller Drehungen die das Quadrat <math>\overline{ABCD}</math> auf sich selbst abbilden:<br />
 +
<math>D_D:=\left\{D_{0}, D_{90}, D_{180}, D_{270}\right\}</math><br /><br />
 +
Die Verknüpfung sei die NAF.<br /><br />
 +
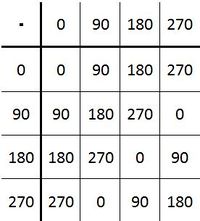
Daraus ergibt sich folgende Verknüpfungstafel:<br />
 +
[[Bild:Verknüpfungstafel_DR.3JPG.JPG| 200px]]<br /><br />
 +
Anmerkung: Die Gruppe der Deckdrehungen des Quadrats ist eine cyklische Gruppe.<br /><br />
 
==Gruppe der Deckabbildungen des Rechtecks==
 
==Gruppe der Deckabbildungen des Rechtecks==
−
 
 
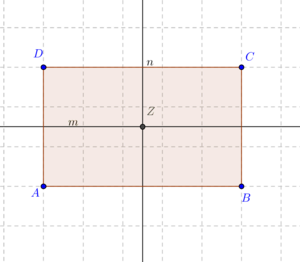
[[Bild:Decvkabbildungen_Rechteck.png| 300px]]<br />
 
[[Bild:Decvkabbildungen_Rechteck.png| 300px]]<br />
 
Unter <math>D_R</math> wollen wir die Menge aller Bewegungen verstehen, die das Rechteck <math>\overline{ABCD}</math> auf sich selbst abbilden. Es handelt sich dabei um die folgenden Drehungen (mit dem Drehzentrum <math>Z</math>) und Geradenspiegelungen:<br />
 
Unter <math>D_R</math> wollen wir die Menge aller Bewegungen verstehen, die das Rechteck <math>\overline{ABCD}</math> auf sich selbst abbilden. Es handelt sich dabei um die folgenden Drehungen (mit dem Drehzentrum <math>Z</math>) und Geradenspiegelungen:<br />
 
<math>D_R:=\left\{D_{0}, D_{180}, S_m, S_n\right\}</math><br /><br />
 
<math>D_R:=\left\{D_{0}, D_{180}, S_m, S_n\right\}</math><br /><br />
 
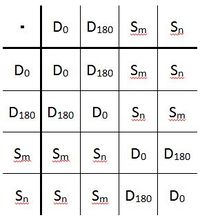
Es ergibt sich folgende Verknüpfungstafel:<br />
 
Es ergibt sich folgende Verknüpfungstafel:<br />
−
[[Bild:Verknüpfungstafel_DR.4.JPG]]
+
[[Bild:Verknüpfungstafel_DR.4.JPG| 200px]]
  
  

Version vom 11. Dezember 2012, 16:17 Uhr


Inhaltsverzeichnis

Beispiele für endliche Gruppen

Restklassen modulo 4

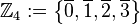
\mathbb{Z}_4:=\left\{ \overline{0}, \overline{1}, \overline{2}, \overline{3} \right\}
mit
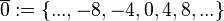\overline{0}:=\left\{..., -8, -4, 0, 4, 8, ...\right\} (Menge aller durch 4 teilbaren ganzen Zahlen),
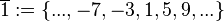\overline{1}:=\left\{..., -7, -3, 1, 5, 9, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 1 lassen),
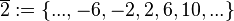\overline{2}:=\left\{..., -6, -2, 2, 6, 10, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 2 lassen),
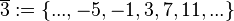\overline{3}:=\left\{..., -5, -1, 3, 7, 11, ...\right\} (Menge aller ganzen Zahlen, die bei Division durch 4 den Rest 3 lassen),

Wir definieren auf \mathbb{Z}_4 eine Verknüpfung \oplus wie folgt:
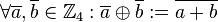
\forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a}\oplus \overline{b} := \overline{a+b}

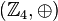Die Struktur \left(\mathbb{Z}_4, \oplus\right) ist eine Gruppe:

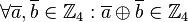  1. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 abgeschlossen, d.h. \forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} \in \mathbb{Z}_4,
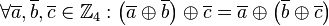  2. Die Verknüpfung \oplus ist auf der Menge \mathbb{Z}_4 assoziativ, d.h. \forall \overline{a}, \overline{b}, \overline{c} \in \mathbb{Z}_4: \left(\overline{a} \oplus \overline{b} \right) \oplus \overline{c}= \overline{a} \oplus \left( \overline{b} \oplus \overline{c} \right),
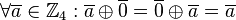  3. \mathbb{Z}_4 hat ein neutrales Element, nämlich die Klasse \overline{0}, d.h. \forall \overline{a} \in \mathbb{Z}_4: \overline{a} \oplus \overline{0}= \overline{0} \oplus \overline{a} = \overline{a},
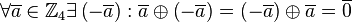  4. Zu jedem Element aus \mathbb{Z}_4 gibt es ein inverses Element, d.h. \forall \overline{a} \in \mathbb{Z}_4 \exist \left(-\overline{a}\right): \overline{a} \oplus \left(-\overline{a}\right) = \left(-\overline{a}\right) \oplus \overline{a} = \overline{0} .

Die folgende Verknüpfungstafel verdeutlicht die obigen Eigenschaften:



Die Tabelle wurde mit der Tabellenkalkulation von Geogebra generiert. Aus diesem Grunde fehlen die Querstriche über den Klassen.

Die Verknüpfungstabelle zeigt eine weitere Eigenschaft der Gruppe \left(\mathbb{Z}_4, \oplus\right):
Die Ergebnisse in der Tabelle sind symmetrisch bezüglich der Hauptdiagonalen angeordnet. Letzteres bedeutet, dass die Verknüpfung \oplus auf \mathbb{Z}_4 kommutativ ist:

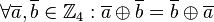  • \forall \overline{a}, \overline{b} \in \mathbb{Z}_4: \overline{a} \oplus \overline{b} = \overline{b} \oplus \overline{a}.

Kommutative Gruppen werden auch Abelsche Gruppen genannt.

Gruppe der Deckdrehungen des Quadrats

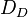Hierbei verstehen wir unter D_D die Menge aller Drehungen die das Quadrat \overline{ABCD} auf sich selbst abbilden:
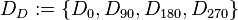
D_D:=\left\{D_{0}, D_{90}, D_{180}, D_{270}\right\}

Die Verknüpfung sei die NAF.

Daraus ergibt sich folgende Verknüpfungstafel:
Verknüpfungstafel DR.3JPG.JPG

Anmerkung: Die Gruppe der Deckdrehungen des Quadrats ist eine cyklische Gruppe.

Gruppe der Deckabbildungen des Rechtecks

Decvkabbildungen Rechteck.png
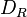Unter D_R wollen wir die Menge aller Bewegungen verstehen, die das Rechteck \overline{ABCD} auf sich selbst abbilden. Es handelt sich dabei um die folgenden Drehungen (mit dem Drehzentrum Z) und Geradenspiegelungen:
D_R:=\left\{D_{0}, D_{180}, S_m, S_n\right\}

Es ergibt sich folgende Verknüpfungstafel:
Verknüpfungstafel DR.4.JPG

Von „http://geometrie.zum.de/index.php?title=Gruppen,_abelsche_Gruppen_2012_12&oldid=19500“