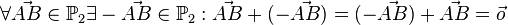Die abelsche Gruppe der Pfeilklassen 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Inverse Elemente) |
*m.g.* (Diskussion | Beiträge) (→Neutrales Element) |
||
| Zeile 10: | Zeile 10: | ||
==Neutrales Element== | ==Neutrales Element== | ||
<math>\exist \vec{o} \in \mathbb{P}_2 :\forall \vec{v} \in \mathbb{P}_2:\vec{o}+ \vec{v}=\vec{v} + \vec{o}=\vec{v}</math><br /> | <math>\exist \vec{o} \in \mathbb{P}_2 :\forall \vec{v} \in \mathbb{P}_2:\vec{o}+ \vec{v}=\vec{v} + \vec{o}=\vec{v}</math><br /> | ||
| − | <math>\exist \vec{o} \in \mathbb{P}_3 :\forall \vec{v} \in \mathbb{P}_3:\vec{o}+ \vec{v}=\vec{v} + \vec{o}=\vec{v}</math> | + | <math>\exist \vec{o} \in \mathbb{P}_3 :\forall \vec{v} \in \mathbb{P}_3:\vec{o}+ \vec{v}=\vec{v} + \vec{o}=\vec{v}</math><br /> |
| + | |||
| + | Die Pfeilklasse des Raumes bzw. der Ebene, die den Nullpfeil enthält, leistet das Verlangte. | ||
==Inverse Elemente== | ==Inverse Elemente== | ||
<math>\forall \vec{AB} \in \mathbb{P}_2 \exist -\vec{AB} \in \mathbb{P}_2: \vec{AB}+(-\vec{AB})=(-\vec{AB})+\vec{AB}=\vec{o}</math> | <math>\forall \vec{AB} \in \mathbb{P}_2 \exist -\vec{AB} \in \mathbb{P}_2: \vec{AB}+(-\vec{AB})=(-\vec{AB})+\vec{AB}=\vec{o}</math> | ||
Version vom 12. Dezember 2012, 17:44 Uhr
Inhaltsverzeichnis |
Die Menge und die Verknüpfung
Wir fassen alle Pfeilklassen des Raumes bzw. der Ebene zu jeweils einer Menge zusammen. Als Verknüpfung wählen wir die Addition von Pfeilklassen. Mit 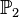 wollen wir die Menge der Pfeilklassen der Ebene bezeichnen, mit
wollen wir die Menge der Pfeilklassen der Ebene bezeichnen, mit 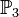 die Menge der Pfeilklassen des Raumes.
die Menge der Pfeilklassen des Raumes.
Die Eigenschaften
Abgeschlossenheit
Die Addition zweier Pfeilklassen der Ebene bzw. des Raumes ist wiederum eine Pfeilklasse der Ebene bzw. des Raumes.
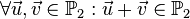
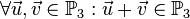
Neutrales Element
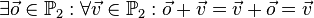
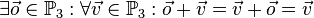
Die Pfeilklasse des Raumes bzw. der Ebene, die den Nullpfeil enthält, leistet das Verlangte.
Inverse Elemente