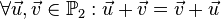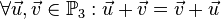Die abelsche Gruppe der Pfeilklassen 2012 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Neutrales Element) |
*m.g.* (Diskussion | Beiträge) |
||
| (15 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> | ||
| + | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- hier drüber nichts eintragen ---> | ||
| + | |||
| + | =Vorbemerkung= | ||
| + | Ich hab das hier mal alles recht abstrakt zusammen getragen. Sinn macht diese Zusammenstellung erst, wenn sie grafisch mittels dynamischer Geometrie unterlegt wird ... .--[[Benutzer:*m.g.*|*m.g.*]] 17:56, 12. Dez. 2012 (CET) | ||
=Die Menge und die Verknüpfung= | =Die Menge und die Verknüpfung= | ||
Wir fassen alle Pfeilklassen des Raumes bzw. der Ebene zu jeweils einer Menge zusammen. Als Verknüpfung wählen wir die Addition von Pfeilklassen. Mit <math>\mathbb{P}_2</math> wollen wir die Menge der Pfeilklassen der Ebene bezeichnen, mit <math>\mathbb{P}_3</math> die Menge der Pfeilklassen des Raumes. | Wir fassen alle Pfeilklassen des Raumes bzw. der Ebene zu jeweils einer Menge zusammen. Als Verknüpfung wählen wir die Addition von Pfeilklassen. Mit <math>\mathbb{P}_2</math> wollen wir die Menge der Pfeilklassen der Ebene bezeichnen, mit <math>\mathbb{P}_3</math> die Menge der Pfeilklassen des Raumes. | ||
| Zeile 7: | Zeile 14: | ||
<math>\forall \vec{u}, \vec{v} \in \mathbb{P}_2: \vec{u} + \vec{v} \in \mathbb{P}_2</math><br /> | <math>\forall \vec{u}, \vec{v} \in \mathbb{P}_2: \vec{u} + \vec{v} \in \mathbb{P}_2</math><br /> | ||
<math>\forall \vec{u}, \vec{v} \in \mathbb{P}_3: \vec{u} + \vec{v} \in \mathbb{P}_3</math> | <math>\forall \vec{u}, \vec{v} \in \mathbb{P}_3: \vec{u} + \vec{v} \in \mathbb{P}_3</math> | ||
| + | ==Assoziativität== | ||
| + | <math>\forall \vec{a}, \vec{b}, \vec{c} \in \mathbb{P}_2: (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})</math><br /> | ||
| + | <math>\forall \vec{a}, \vec{b}, \vec{c} \in \mathbb{P}_2: (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})</math> | ||
==Neutrales Element== | ==Neutrales Element== | ||
| − | <math>\exist \vec{o} \in mathbb{P}_2:\forall \vec{v} \in mathbb{P}_2:\vec{o}+ \vec{v}=\vec{v} + \vec{o}=\vec{v}</math> | + | <math>\exist \vec{o} \in \mathbb{P}_2 :\forall \vec{v} \in \mathbb{P}_2:\vec{o}+ \vec{v}=\vec{v} + \vec{o}=\vec{v}</math><br /> |
| + | <math>\exist \vec{o} \in \mathbb{P}_3 :\forall \vec{v} \in \mathbb{P}_3:\vec{o}+ \vec{v}=\vec{v} + \vec{o}=\vec{v}</math><br /> | ||
| + | |||
| + | Die Pfeilklasse des Raumes bzw. der Ebene, die den Nullpfeil enthält, leistet das Verlangte. | ||
==Inverse Elemente== | ==Inverse Elemente== | ||
| − | <math>\forall \vec{ | + | <math>\forall \vec{u} \in \mathbb{P}_2 \exist -\vec{u} \in \mathbb{P}_2: \vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\vec{o}</math><br /> |
| + | <math>\forall \vec{u} \in \mathbb{P}_3 \exist -\vec{u} \in \mathbb{P}_3: \vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\vec{o}</math><br /> | ||
| + | |||
| + | Das inverse Element zur Pfeilklasse mit dem Repräsentanten <math>\vec{AB}</math> ist die Pfeilklasse mit dem Repräsentanten <math>\vec{BA}</math>. <br />(Sowohl im Raum als auch in der Ebene). | ||
| + | ==Fazit 1== | ||
| + | <math>\left(\mathbb{P}_2, +\right)</math> ist Gruppe,<br /> | ||
| + | <math>\left(\mathbb{P}_3, +\right)</math> ist Gruppe, | ||
| + | |||
| + | ==Kommutativität== | ||
| + | <math>\forall \vec{u}, \vec{v} \in \mathbb{P}_2: \vec{u}+\vec{v}=\vec{v}+\vec{u}</math><br /> | ||
| + | <math>\forall \vec{u}, \vec{v} \in \mathbb{P}_3: \vec{u}+\vec{v}=\vec{v}+\vec{u}</math> | ||
| + | ==Fazit 2== | ||
| + | <math>\left(\mathbb{P}_2, +\right)</math> ist abelsche Gruppe,<br /> | ||
| + | <math>\left(\mathbb{P}_3, +\right)</math> ist abelsche Gruppe. | ||
| + | |||
| + | <!--- hier drunter nichts eintragen ---> | ||
| + | [[Kategorie:Linalg]] | ||
| + | |||
| + | |} | ||
| + | </div> | ||
Aktuelle Version vom 12. Dezember 2012, 17:57 Uhr
VorbemerkungIch hab das hier mal alles recht abstrakt zusammen getragen. Sinn macht diese Zusammenstellung erst, wenn sie grafisch mittels dynamischer Geometrie unterlegt wird ... .--*m.g.* 17:56, 12. Dez. 2012 (CET) Die Menge und die VerknüpfungWir fassen alle Pfeilklassen des Raumes bzw. der Ebene zu jeweils einer Menge zusammen. Als Verknüpfung wählen wir die Addition von Pfeilklassen. Mit Die EigenschaftenAbgeschlossenheitDie Addition zweier Pfeilklassen der Ebene bzw. des Raumes ist wiederum eine Pfeilklasse der Ebene bzw. des Raumes. Assoziativität
Neutrales Element
Die Pfeilklasse des Raumes bzw. der Ebene, die den Nullpfeil enthält, leistet das Verlangte. Inverse Elemente
Das inverse Element zur Pfeilklasse mit dem Repräsentanten Fazit 1
Kommutativität
Fazit 2
|
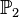 wollen wir die Menge der Pfeilklassen der Ebene bezeichnen, mit
wollen wir die Menge der Pfeilklassen der Ebene bezeichnen, mit 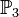 die Menge der Pfeilklassen des Raumes.
die Menge der Pfeilklassen des Raumes.
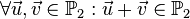
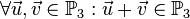
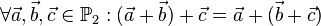
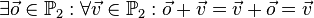
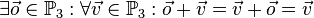
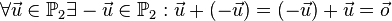
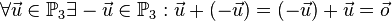
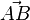 ist die Pfeilklasse mit dem Repräsentanten
ist die Pfeilklasse mit dem Repräsentanten 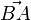 .
. 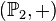 ist Gruppe,
ist Gruppe,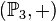 ist Gruppe,
ist Gruppe,