Strahlen bzw. Halbgeraden WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Definition II.5: (Halbgerade, bzw. Strahl)) |
*m.g.* (Diskussion | Beiträge) (→Definition II.5: (Halbgerade, bzw. Strahl)) |
||
| (11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
| + | |||
| + | |||
| + | |||
= Halbgeraden bzw. Strahlen = | = Halbgeraden bzw. Strahlen = | ||
===== Geogebra-App ===== | ===== Geogebra-App ===== | ||
*Verschieben Sie <math>P</math> auf <math>AB</math> | *Verschieben Sie <math>P</math> auf <math>AB</math> | ||
| − | *Manipulieren Sie <math>A</math> und <math>B</math> für eine andere | + | *Manipulieren Sie <math>A</math> und <math>B</math> für eine andere Lage der Geraden <math>AB</math> |
| Zeile 9: | Zeile 17: | ||
===== Definition II.5: (Halbgerade, bzw. Strahl) ===== | ===== Definition II.5: (Halbgerade, bzw. Strahl) ===== | ||
| − | {{Definition|'''Halbgerade <math>AB^+</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^+</math> versteht man die Menge aller Punkte <math>P</math> für die gilt: <br />(a) | + | (Ergänzen Sie die fehlenden Teile selbst.)<br /> |
| − | {{Definition|'''Halbgerade <math>AB^-</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^-</math> versteht man die Menge aller Punkte <math>P</math> für die gilt: ... }} | + | {{Definition|'''offene Halbgerade <math>AB^+</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^+</math> versteht man die Menge aller Punkte <math>P</math> für die gilt: <br />(a) Zw(A,P,B) <br /> oder <br />(b) Zw(A,B,P)<br />Der Punkt <math>A</math> heißt Anfangspunkt von <math>AB^+</math>.}} |
| + | {{Definition|'''offene Halbgerade <math>AB^-</math>'''<br />Es sei <math>AB</math> eine Gerade. Unter der offenen Halbgeraden <math>AB^-</math> versteht man die Menge aller Punkte <math>P</math> für die gilt: Zw (P,A,B) <br />Der Punkt <math>A</math> heißt Anfangspunkt von <math>AB^-</math>.}} | ||
| + | {{Definition|'''Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math>'''<br /> Es sei <math>AB</math> eine Gerade. Unter den Halbgeraden <math>AB^+</math> bzw. <math>AB^-</math> versteht man die offenen Halbgeraden <math>AB+</math> bzw. <math>AB^-</math> jeweils vereinigt mit den Punkten A und B. }}<br/> | ||
| + | |||
| + | Bei der offenen Halbgeraden AB+ muss noch der Punkt B dazu! | ||
| + | --[[Benutzer:Caro44|Caro44]] 16:05, 8. Dez. 2012 (CET)<br /> | ||
| + | korrekt --[[Benutzer:*m.g.*|*m.g.*]] 17:56, 15. Dez. 2012 (CET) | ||
| + | |||
| + | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | [[Category:Einführung_S]] | ||
Aktuelle Version vom 15. Dezember 2012, 17:56 Uhr
|
Halbgeraden bzw. StrahlenGeogebra-App
Definition II.5: (Halbgerade, bzw. Strahl)(Ergänzen Sie die fehlenden Teile selbst.) Definition offene Halbgerade Definition offene Halbgerade Definition Halbgeraden Bei der offenen Halbgeraden AB+ muss noch der Punkt B dazu!
--Caro44 16:05, 8. Dez. 2012 (CET) |
 auf
auf 
 und
und  für eine andere Lage der Geraden
für eine andere Lage der Geraden 

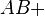 bzw.
bzw. 
