Lösung von Aufgabe 10.4P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.4: Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.<br /> Kategorie:Einführung_P“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | Beweisen Sie Satz IX. | + | Beweisen Sie Satz IX.3: |
| − | Bei einer Punktspiegelung | + | Bei einer Punktspiegelung ist der Schnittpunkt ''S'' der beiden Spiegelgeraden ''a'' und ''b'' Mittelpunkt der Strecke <math>\overline{PP''}</math>, mit <math>P''=a\circ b(P) </math>.<br /> |
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 17. Januar 2013, 13:26 Uhr
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 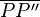 , mit
, mit 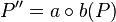 .
.

