Lösung von Aufg. 10.2 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Lösung von User ...) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 18:53, 19. Jan. 2013 (CET)) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
::Wenn ein Punkt <math>\ P</math> zu den Endpunkten der Strecke <math>\overline{AB}</math> jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von <math>\overline{AB}</math>. | ::Wenn ein Punkt <math>\ P</math> zu den Endpunkten der Strecke <math>\overline{AB}</math> jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von <math>\overline{AB}</math>. | ||
=Lösung von User ...= | =Lösung von User ...= | ||
| − | [[Datei:10.2.JPG|500px|]]<br --[[Benutzer:B.....|B.....]] 21:42, 16. Jan. 2013 (CET) | + | [[Datei:10.2.JPG|500px|]]<br /> |
| + | --[[Benutzer:B.....|B.....]] 21:42, 16. Jan. 2013 (CET) | ||
| + | ==Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 18:53, 19. Jan. 2013 (CET)== | ||
| + | Prinzipiell richtig. Feintuning:<br /> | ||
| + | <u>Fall 1:</u> <math>P</math> liegt auf <math>\overline{AB}</math><br /> | ||
| + | ::In diesem Fall ist <math>P</math> der Mittelpunkt von <math>\overline{AB}</math> und somit ist <math>P</math> ein Punkt der Mittelsenkrechten von <math>\overline{AB}</math>.<br /> | ||
| + | <u>Fall 2:</u> <math>P</math> liegt nicht auf <math>\overline{AB}</math>. <math>M</math> sei jetzt der Mittelpunkt von <math>\overline{AB}</math> | ||
=Lösung von User ...= | =Lösung von User ...= | ||
Aktuelle Version vom 19. Januar 2013, 18:55 Uhr
Aufgabe 10.2Beweisen Sie Satz VII.6 a:
Lösung von User ...
Bemerkung --*m.g.* 18:53, 19. Jan. 2013 (CET)Prinzipiell richtig. Feintuning:
Fall 2: Lösung von User ... |
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von 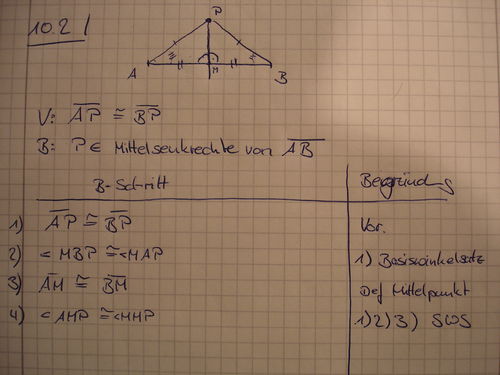
 liegt auf
liegt auf  sei jetzt der Mittelpunkt von
sei jetzt der Mittelpunkt von 
