Lösung von Aufg. 10.5 WS 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 15:56, 20. Jan. 2013 (CET)) |
|||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
P und Q sind paarweise verschiedene Punkte. <math>\overline{AP} </math> = <math> \overline{PB}\ \wedge \ \overline{AQ} </math> = <math>\overline{QB} </math>. | P und Q sind paarweise verschiedene Punkte. <math>\overline{AP} </math> = <math> \overline{PB}\ \wedge \ \overline{AQ} </math> = <math>\overline{QB} </math>. | ||
Nach Axiom I.1 bildet P, Q eine ''Gerade g''. Die ''Gerade g'' ist die Mittelsenkrechte der Strecke <math>\overline{AB}</math> . | Nach Axiom I.1 bildet P, Q eine ''Gerade g''. Die ''Gerade g'' ist die Mittelsenkrechte der Strecke <math>\overline{AB}</math> . | ||
| + | |||
| + | ==Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 17:10, 19. Jan. 2013 (CET)== | ||
| + | Das beantwortet die Frage noch nicht ganz.<br /> | ||
| + | Sie sagen: Wenn du zwei Punkte hast die beide jeweils ein und denselben Abstand zu den Endpunkten einer Strecke haben, dann hast du mit den beiden Punkten auch die durch die Punkte eindeutig bestimmte Gerade, welche dann die Mittelsenkrechte der Strecke ist. Das ganze lässt sich sicherlich noch mehr als Definition formulieren.<br /> | ||
| + | Der Knackpunkt ist jetzt aber: Warum dürfen wir auf dies Art und Weise den Begriff der Mittelsenkrechte formulieren?<br /> | ||
| + | Tipp: Eine definierende Eigenschaft muss immer notwendig und hinreichend sein. Bedingungen, die sowohl notwendig als auch hinreichend sind, werden Kriterien genannt.<br /> | ||
| + | Das Inzidenzaxiom wurde sicherlich korrekt angewendet, liefert aber nicht die eigentliche Begründung dafür, dass unsere Gerade die Mittelsenkrechte ist.<br /> | ||
| + | Versuchen Sie es einmal mit: Die Mittelsenkrechte einer Strecke ist die Menge aller Punkte, die ... . | ||
=Lösung von User ...= | =Lösung von User ...= | ||
| − | + | Die Mittelsenkrechte einer Strecke ist die Menge aller Punkte, die zu den Endpunkten der Strecke ein und denselben Abstand. --LilPonsho 12:56, 20. Jan. 2013 (CET) | |
| − | + | ==Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 15:56, 20. Jan. 2013 (CET)== | |
| + | Besser: ..., die zu den Endpunkten der Strecke ''jeweils'' ein und denselben Abstand hat. (Ansonsten ließe es sich so interpretieren, dass der Abstand für alle Punkte immer derselbe sein müßte.) | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
Aktuelle Version vom 20. Januar 2013, 15:56 Uhr
--
Aufgabe 10.5Erläutern Sie, wie und warum sich aus den Satz VII.6 eine neue Möglichkeit, der Definition des Begriffs der Mittelsenkrechte ergibt. Lösung von Mr. Private 15:10, 19. Jan. 2013 (CET)Sei = Nach Axiom I.1 bildet P, Q eine Gerade g. Die Gerade g ist die Mittelsenkrechte der Strecke Bemerkung --*m.g.* 17:10, 19. Jan. 2013 (CET)Das beantwortet die Frage noch nicht ganz. Lösung von User ...Die Mittelsenkrechte einer Strecke ist die Menge aller Punkte, die zu den Endpunkten der Strecke ein und denselben Abstand. --LilPonsho 12:56, 20. Jan. 2013 (CET) Bemerkung --*m.g.* 15:56, 20. Jan. 2013 (CET)Besser: ..., die zu den Endpunkten der Strecke jeweils ein und denselben Abstand hat. (Ansonsten ließe es sich so interpretieren, dass der Abstand für alle Punkte immer derselbe sein müßte.) |
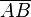 eine Strecke.
P und Q sind paarweise verschiedene Punkte.
eine Strecke.
P und Q sind paarweise verschiedene Punkte. 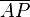 = Fehler beim Parsen(Lexikalischer Fehler): \overline{PB}\ \wedge \ \overline{AQ}
= Fehler beim Parsen(Lexikalischer Fehler): \overline{PB}\ \wedge \ \overline{AQ}
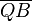 .
.
 .
.

