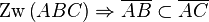Videos von Studierenden: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
HecklF (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Und das passende Pendant \ AB^{-} gleich dazu) |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
== Und das passende Pendant <math>\ AB^{-}</math> gleich dazu == | == Und das passende Pendant <math>\ AB^{-}</math> gleich dazu == | ||
| − | |||
| + | {{#ev:youtube|CINPcNkPWDo}} | ||
Die Videos wurden in der Tat spontan erstellt, helfen aber evtl. ein wenig fürs Verständnis. --[[Benutzer:HecklF|Flo60]] 19:32, 10. Jun. 2011 (CEST) | Die Videos wurden in der Tat spontan erstellt, helfen aber evtl. ein wenig fürs Verständnis. --[[Benutzer:HecklF|Flo60]] 19:32, 10. Jun. 2011 (CEST) | ||
| Zeile 11: | Zeile 11: | ||
Leider können Videos dieses Formates nicht direkt ins Wiki hochgeladen werden - deshalb muss man es erst aus dem zip-Format entpacken. --[[Benutzer:HecklF|Flo60]] 23:59, 30. Okt. 2011 (CET) | Leider können Videos dieses Formates nicht direkt ins Wiki hochgeladen werden - deshalb muss man es erst aus dem zip-Format entpacken. --[[Benutzer:HecklF|Flo60]] 23:59, 30. Okt. 2011 (CET) | ||
| + | ==Lösung von Übungsaufgabe 5.2 des Sommersemesters 2012== | ||
| + | Die Aufgabe: Man beweise: <math>\operatorname{Zw}\left(ABC\right) \Rightarrow \overline{AB} \subset \overline{AC}</math> | ||
| + | {{#ev:youtube|LCRLc6f2fPs}} | ||
| + | ==Lösung von Aufgabe 8.6 b Wintersemester 2012_13== | ||
| + | {{#ev:youtube|LCTHgm1wlBU}} | ||
Aktuelle Version vom 21. Januar 2013, 22:00 Uhr
Inhaltsverzeichnis |
Eine etwas andere Darstellung von 
Und das passende Pendant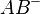 
gleich dazu
Die Videos wurden in der Tat spontan erstellt, helfen aber evtl. ein wenig fürs Verständnis. --Flo60 19:32, 10. Jun. 2011 (CEST)
Spiegelung eines Punktes an einer Geraden
Leider können Videos dieses Formates nicht direkt ins Wiki hochgeladen werden - deshalb muss man es erst aus dem zip-Format entpacken. --Flo60 23:59, 30. Okt. 2011 (CET)
Lösung von Übungsaufgabe 5.2 des Sommersemesters 2012
Die Aufgabe: Man beweise: 
