Umkehrung des Stufenwinkelsatzes (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 17:34, 24. Jan. 2013 (CET)) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 17:34, 24. Jan. 2013 (CET)) |
||
| Zeile 39: | Zeile 39: | ||
Nur für ganz Pingelige: so wie (7) formuliert wurde handelt es sich nicht explizit um eine Gleichung. Hinter (7) verbirgt sich jedoch eine Gleichung: <math>|\beta|=|\angle SBA|</math>.<br /> | Nur für ganz Pingelige: so wie (7) formuliert wurde handelt es sich nicht explizit um eine Gleichung. Hinter (7) verbirgt sich jedoch eine Gleichung: <math>|\beta|=|\angle SBA|</math>.<br /> | ||
| − | + | ||
Version vom 24. Januar 2013, 17:35 Uhr
|
Stufenwinkel, Wechselwinkel, entgegengesetzt liegende WinkelZeichnen Sie Bespiele und Gegenbeispiele zu den in der Überschrift genannten Begriffen und laden Sie Ihre Zeichnungen hier mit entsprechenden Kommentaren hoch. Die Umkehrung des StufenwinkelsatzesSatz X.1: (Umkehrung des Stufenwinkelsatzes)
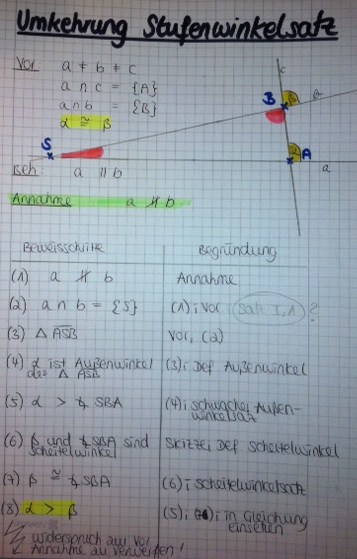
Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)Es seien Voraussetzung: (i) Behauptung:
Annahme:
Den Rest können Sie selbst! Beweisführung Caro44
Bemerkung --*m.g.* 17:34, 24. Jan. 2013 (CET)sehr gut! Nur für ganz Pingelige: so wie (7) formuliert wurde handelt es sich nicht explizit um eine Gleichung. Hinter (7) verbirgt sich jedoch eine Gleichung:
|
 und
und  zwei nicht identische Geraden, die durch eine dritte Gerade
zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner
jeweils geschnitten werden. Es seien ferner  und
und  zwei Stufenwinkel, die bei dem Schnitt von
zwei Stufenwinkel, die bei dem Schnitt von 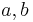 und
und  und die Gerade
und die Gerade  schneiden.
schneiden. 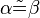
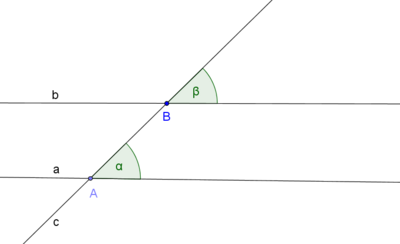
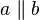
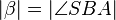 .
.
