Serie 12 (WS 12 13): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 12.01) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 12.09) |
||
| (32 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
=Aufgabe 12.01= | =Aufgabe 12.01= | ||
Auf einem Blatt Papier sei eine Strecke <math>\overline{AB}</math> gegeben. Die Schüler falten das Blatt so, dass <math>A</math> mit <math>B</math> zur Deckung kommt. Was ist die Faltgerade bezüglich der Strecke <math>\overline{AB}</math>. Begründen Sie ihre Antwort. Begründen ist im Sinne von Plausibilitätserklärungen zu verstehen, ein echter Beweis ist im Rahmen der Einführung in die Geometrie nicht möglich.) | Auf einem Blatt Papier sei eine Strecke <math>\overline{AB}</math> gegeben. Die Schüler falten das Blatt so, dass <math>A</math> mit <math>B</math> zur Deckung kommt. Was ist die Faltgerade bezüglich der Strecke <math>\overline{AB}</math>. Begründen Sie ihre Antwort. Begründen ist im Sinne von Plausibilitätserklärungen zu verstehen, ein echter Beweis ist im Rahmen der Einführung in die Geometrie nicht möglich.) | ||
| + | |||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.01 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.02= | ||
| + | Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt.<br /> | ||
| + | Dass sich zwei Mittelsenkrechten eines Dreieck in genau einem Punkt schneiden dürfen Sie voraussetzen. | ||
| + | |||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.02 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.03= | ||
| + | In der vorangegangenen Übungsserie haben wir zwei Aufgaben zu Winkelhalbierenden gelöst. Diese Aufgaben bilden die Grundlage für ein Winkelhalbierendenkriterium. Ergänzen Sie dieses:<br /> | ||
| + | Ein Punkt P gehört genau dann zur Winkelhalbierenden eines Winkels <math>\alpha</math>, wenn ... | ||
| + | |||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.03 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.04= | ||
| + | Beweisen Sie: Die Winkelhalbierenden eines Dreiecks schneiden sie in genau einem Punkt.<br /> | ||
| + | Dass sich zwei Winkelhalbierende eines Dreieck in genau einem Punkt schneiden dürfen Sie voraussetzen. | ||
| + | |||
| + | [[Lösung von Aufgabe 12.04 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.05= | ||
| + | {{Definition|Parallelogramm<br />Ein Parallelogramm ist ein Viereck mit zwei Paaren paralleler Seiten.}} | ||
| + | Beweisen Sie ohne Verwendung weiterer aus der Schule bekannten Eigenschaften von Parallelogrammen:<br /> | ||
| + | <math>\overline{ABCD}</math> ist ein Parallelogramm <math>\Leftrightarrow \overline{AB} \tilde= \overline{CD} \wedge \overline{AD} \tilde= \overline{BC}</math>. | ||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.05 WS_12_13]] | ||
| + | =Aufgabe 12.06= | ||
| + | Beweisen Sie: Die Höhen eines Dreiecks (bzw. die Geraden, die durch die Höhen eindeutig bestimmt sind) schneiden einander in genau einem Punkt.<br /> | ||
| + | Hilfe: Es sei <math>\overline{ABC}</math> ein Dreieck. Von diesem Dreieck wissen Sie bereits, dass sich seine Mittelsenkrechten in genau einem Punkt schneiden. Konstruieren aus <math>\overline{ABC}</math> ein weiteres Dreieck, indem sie die drei Parallelen konstruieren, die sie erhalten, wenn sie die Parallele jeweils durch einen Eckpunkt von <math>\overline{ABC}</math> zur gegenüberliegenden Seite legen. | ||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.06 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.07= | ||
| + | Lisa lässt ihre Schüler Vierecke generieren. Hierzu gibt sie ihnen einen Streifen (n cm breies Pappstück, dessen gegenüberliegende Seiten parallel sind, das Paar von gegenüberliegenden Seiten mit dem Abstand n cm ist blau gekennzeichnet) und Stäbchen. Die Aufgabe lautet: Lege jeweils ein Paar gleichlanger Stäbchen so, dass beide Enden der Stäbchen jeweils auf einer der blauen Seite liegen, so dass Vierecke entstehen. Lege so dass zwar Rechtecke aber keine beliebigen Parallelogramme entstehen.<br /> | ||
| + | Benennen und definieren Sie den Viereckstyp, der sich durch diese Tätigkeit ergibt. Die Definition darf nur auf der Grundlage der geschilderten Schülertätigkeit formuliert werden. | ||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.07 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.08= | ||
| + | Sie wissen im Folgenden nicht mehr und nicht weniger über Parallelogramme, als dass diese Vierecke mit zwei Paaren zueinander paralleler Seiten sind und dass die gegenüberliegenden Seiten diese Vierecke kongruent zueinander sind.Rauten sind für Sie Parallelogramme, in denen alle Seiten gleichlang sind.<br /><br /> | ||
| + | Es sei <math>\overline{ABCD}</math> ein Parallelogramm mit <math>|AB|=|CD|=a</math> und <math>|AD|=|BC|=b</math> und <math>a>b</math>. | ||
| + | |||
| + | Es sei <math>w_{\alpha}</math> die Winkelhalbierende des Winkels <math>\angle BAD</math>, <math>w_{\delta}</math> sei die Winkelhalbierende des Winkels <math>\angle ADC</math>. Sie dürfen davon ausgehen, dass <math>w_{\alpha}</math> <math>DC</math> im Punkt <math>C'</math> schneidet. Analog schneidet <math>w_{\delta}</math> <math>AB</math> in <math>B'</math>. | ||
| + | |||
| + | Beweisen Sie <math>\overline{AB'C'D}</math> ist eine Raute. | ||
| + | |||
| + | [[Lösung von Aufgabe 12.08 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.09= | ||
| + | Es sei <math>k</math> ein Kreis und <math>\overline{MB}</math> ein Radius von <math>k</math>. <math>t</math> sei eine Gerade mit <math>t \perp MB \wedge B \in t</math>. Beweisen Sie <math>\neg \exist P: P \in t \wedge P \in k \wedge P \not \equi B</math>. | ||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.09 WS_12_13]] | ||
| + | |||
| + | =Aufgabe 12.10= | ||
| + | Ebene Geometrie: | ||
| + | Es sei <math>k</math> ein Kreis und <math>t</math> eine Gerade mit <math>k \cap t =\{B\}</math>. Beweisen Sie: <math>MB \perp t</math>. | ||
| + | |||
| + | |||
| + | [[Lösung von Aufgabe 12.10 WS_12_13]] | ||
Aktuelle Version vom 27. Januar 2013, 16:49 Uhr
Inhaltsverzeichnis |
Hilfe für die Umkreisaufgaben
Aufgabe 12.01
Auf einem Blatt Papier sei eine Strecke  gegeben. Die Schüler falten das Blatt so, dass
gegeben. Die Schüler falten das Blatt so, dass  mit
mit  zur Deckung kommt. Was ist die Faltgerade bezüglich der Strecke
zur Deckung kommt. Was ist die Faltgerade bezüglich der Strecke  . Begründen Sie ihre Antwort. Begründen ist im Sinne von Plausibilitätserklärungen zu verstehen, ein echter Beweis ist im Rahmen der Einführung in die Geometrie nicht möglich.)
. Begründen Sie ihre Antwort. Begründen ist im Sinne von Plausibilitätserklärungen zu verstehen, ein echter Beweis ist im Rahmen der Einführung in die Geometrie nicht möglich.)
Lösung von Aufgabe 12.01 WS_12_13
Aufgabe 12.02
Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt.
Dass sich zwei Mittelsenkrechten eines Dreieck in genau einem Punkt schneiden dürfen Sie voraussetzen.
Lösung von Aufgabe 12.02 WS_12_13
Aufgabe 12.03
In der vorangegangenen Übungsserie haben wir zwei Aufgaben zu Winkelhalbierenden gelöst. Diese Aufgaben bilden die Grundlage für ein Winkelhalbierendenkriterium. Ergänzen Sie dieses:
Ein Punkt P gehört genau dann zur Winkelhalbierenden eines Winkels  , wenn ...
, wenn ...
Lösung von Aufgabe 12.03 WS_12_13
Aufgabe 12.04
Beweisen Sie: Die Winkelhalbierenden eines Dreiecks schneiden sie in genau einem Punkt.
Dass sich zwei Winkelhalbierende eines Dreieck in genau einem Punkt schneiden dürfen Sie voraussetzen.
Lösung von Aufgabe 12.04 WS_12_13
Aufgabe 12.05
Definition
Parallelogramm
Ein Parallelogramm ist ein Viereck mit zwei Paaren paralleler Seiten.
Beweisen Sie ohne Verwendung weiterer aus der Schule bekannten Eigenschaften von Parallelogrammen:
 ist ein Parallelogramm
ist ein Parallelogramm 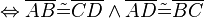 .
.
Lösung von Aufgabe 12.05 WS_12_13
Aufgabe 12.06
Beweisen Sie: Die Höhen eines Dreiecks (bzw. die Geraden, die durch die Höhen eindeutig bestimmt sind) schneiden einander in genau einem Punkt.
Hilfe: Es sei  ein Dreieck. Von diesem Dreieck wissen Sie bereits, dass sich seine Mittelsenkrechten in genau einem Punkt schneiden. Konstruieren aus
ein Dreieck. Von diesem Dreieck wissen Sie bereits, dass sich seine Mittelsenkrechten in genau einem Punkt schneiden. Konstruieren aus  ein weiteres Dreieck, indem sie die drei Parallelen konstruieren, die sie erhalten, wenn sie die Parallele jeweils durch einen Eckpunkt von
ein weiteres Dreieck, indem sie die drei Parallelen konstruieren, die sie erhalten, wenn sie die Parallele jeweils durch einen Eckpunkt von  zur gegenüberliegenden Seite legen.
zur gegenüberliegenden Seite legen.
Lösung von Aufgabe 12.06 WS_12_13
Aufgabe 12.07
Lisa lässt ihre Schüler Vierecke generieren. Hierzu gibt sie ihnen einen Streifen (n cm breies Pappstück, dessen gegenüberliegende Seiten parallel sind, das Paar von gegenüberliegenden Seiten mit dem Abstand n cm ist blau gekennzeichnet) und Stäbchen. Die Aufgabe lautet: Lege jeweils ein Paar gleichlanger Stäbchen so, dass beide Enden der Stäbchen jeweils auf einer der blauen Seite liegen, so dass Vierecke entstehen. Lege so dass zwar Rechtecke aber keine beliebigen Parallelogramme entstehen.
Benennen und definieren Sie den Viereckstyp, der sich durch diese Tätigkeit ergibt. Die Definition darf nur auf der Grundlage der geschilderten Schülertätigkeit formuliert werden.
Lösung von Aufgabe 12.07 WS_12_13
Aufgabe 12.08
Sie wissen im Folgenden nicht mehr und nicht weniger über Parallelogramme, als dass diese Vierecke mit zwei Paaren zueinander paralleler Seiten sind und dass die gegenüberliegenden Seiten diese Vierecke kongruent zueinander sind.Rauten sind für Sie Parallelogramme, in denen alle Seiten gleichlang sind.
Es sei  ein Parallelogramm mit
ein Parallelogramm mit 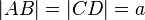 und
und 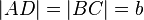 und
und 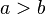 .
.
Es sei 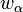 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels 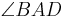 ,
, 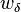 sei die Winkelhalbierende des Winkels
sei die Winkelhalbierende des Winkels 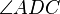 . Sie dürfen davon ausgehen, dass
. Sie dürfen davon ausgehen, dass 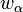
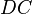 im Punkt
im Punkt 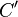 schneidet. Analog schneidet
schneidet. Analog schneidet 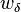
 in
in 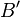 .
.
Beweisen Sie 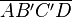 ist eine Raute.
ist eine Raute.
Lösung von Aufgabe 12.08 WS_12_13
Aufgabe 12.09
Es sei  ein Kreis und
ein Kreis und  ein Radius von
ein Radius von  .
.  sei eine Gerade mit
sei eine Gerade mit 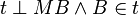 . Beweisen Sie Fehler beim Parsen(Unbekannte Funktion „\equi“): \neg \exist P: P \in t \wedge P \in k \wedge P \not \equi B
.
. Beweisen Sie Fehler beim Parsen(Unbekannte Funktion „\equi“): \neg \exist P: P \in t \wedge P \in k \wedge P \not \equi B
.
Lösung von Aufgabe 12.09 WS_12_13
Aufgabe 12.10
Ebene Geometrie:
Es sei  ein Kreis und
ein Kreis und  eine Gerade mit
eine Gerade mit 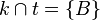 . Beweisen Sie:
. Beweisen Sie: 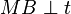 .
.

