Lösung von Aufgabe 12.03 WS 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="background…“) |
Caro44 (Diskussion | Beiträge) (→Lösung User ...) |
||
| (11 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| + | =Aufgabe 12.03= | ||
| + | In der vorangegangenen Übungsserie haben wir zwei Aufgaben zu Winkelhalbierenden gelöst. Diese Aufgaben bilden die Grundlage für ein Winkelhalbierendenkriterium. Ergänzen Sie dieses:<br /> | ||
| + | Ein Punkt P gehört genau dann zur Winkelhalbierenden eines Winkels <math>\alpha</math>, wenn ... | ||
| + | =Lösung User ...= | ||
| + | Pg den selben Abstand zu Ph hat. g und h sein die Schenkel des Winkels. | ||
| + | --[[Benutzer:Yellow|Yellow]] 21:21, 26. Jan. 2013 (CET) | ||
| − | + | @Yellow: Fehlt hier nicht noch die Informationen, das Pg senkrecht auf der Winkelhalbierenden steht? | |
| + | Versuchen Sie es einfach mal ohne die Punkte <math>P_g, P_h</math> aus den Übungsaufgaben. Es waren die Fußpunkte der Lote von <math>P</math> auf die Schenkel des Winkels. Die Länge der Lote von P auf die Schenkel ist jeweils der .... von P zu den Schenkeln.--[[Benutzer:*m.g.*|*m.g.*]] 22:58, 27. Jan. 2013 (CET) | ||
| + | |||
| + | |||
| + | |||
| + | ... wenn die Winkelhalbierende den selben Abstand zu den Schenkeln von alpha hat. | ||
| + | |||
| + | |||
| + | Ein Punkt P gehört genau dann zur Winkelhalbierenden eines Winkels <math>\alpha</math> , wenn P im Inneren von <math>\alpha</math> liegt und jeweils zu den beiden Schenkeln von <math>\alpha</math> ein und denselben Abstand hat. --[[Benutzer:Caro44|Caro44]] 12:19, 29. Jan. 2013 (CET) | ||
=Lösung User ...= | =Lösung User ...= | ||
| + | |||
| + | |||
Aktuelle Version vom 29. Januar 2013, 12:20 Uhr
Aufgabe 12.03In der vorangegangenen Übungsserie haben wir zwei Aufgaben zu Winkelhalbierenden gelöst. Diese Aufgaben bilden die Grundlage für ein Winkelhalbierendenkriterium. Ergänzen Sie dieses: Lösung User ...Pg den selben Abstand zu Ph hat. g und h sein die Schenkel des Winkels. --Yellow 21:21, 26. Jan. 2013 (CET)
... wenn die Winkelhalbierende den selben Abstand zu den Schenkeln von alpha hat.
Lösung User ... |
 , wenn ...
, wenn ...
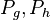 aus den Übungsaufgaben. Es waren die Fußpunkte der Lote von
aus den Übungsaufgaben. Es waren die Fußpunkte der Lote von  auf die Schenkel des Winkels. Die Länge der Lote von P auf die Schenkel ist jeweils der .... von P zu den Schenkeln.--
auf die Schenkel des Winkels. Die Länge der Lote von P auf die Schenkel ist jeweils der .... von P zu den Schenkeln.--
