Lösung von Aufgabe 12.06 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Bemerkungen --*m.g.* 09:48, 31. Jan. 2013 (CET)) |
*m.g.* (Diskussion | Beiträge) (→Bemerkungen --*m.g.* 09:48, 31. Jan. 2013 (CET)) |
||
| Zeile 25: | Zeile 25: | ||
# Das Parallelenaxiom können Sie nicht zur Begründung der Konstruktion der Parallelen verwenden. Grund: Das Parallelenaxiom fordert nicht die Existenz von Parallelen. Es bezieht sich lediglich auf die Eindeutigkeit der Parallelen. Bereits in der absoluten Geometrie können wir zeigen: Durch jeden Punkt<math> P</math> außerhalb einer Geraden <math>g</math> geht eine zu <math>g</math> parallele Gerade <math>h</math>. Was wir nicht beweisen können und deshalb axiomatisch fordern, ist die Tatsache, dass es höchstens eine solche Gerade geben kann. | # Das Parallelenaxiom können Sie nicht zur Begründung der Konstruktion der Parallelen verwenden. Grund: Das Parallelenaxiom fordert nicht die Existenz von Parallelen. Es bezieht sich lediglich auf die Eindeutigkeit der Parallelen. Bereits in der absoluten Geometrie können wir zeigen: Durch jeden Punkt<math> P</math> außerhalb einer Geraden <math>g</math> geht eine zu <math>g</math> parallele Gerade <math>h</math>. Was wir nicht beweisen können und deshalb axiomatisch fordern, ist die Tatsache, dass es höchstens eine solche Gerade geben kann. | ||
#Die korrekte Begründung der Parallelen muss also lauten: Existenz der Parallelen. | #Die korrekte Begründung der Parallelen muss also lauten: Existenz der Parallelen. | ||
| − | # Die weitere Lösung ist nicht ganz korrekt begründet | + | # Die weitere Lösung ist nicht ganz korrekt begründet: Nur mit dem Wechselwinkelsatz werden Sie die Kongruenz der Winkel nicht begründen können, Sie werden auch den Stufenwinkelsatz einsetzen müssen. Die Kongruenz der äußeren Dreiecke zueinander kann man nur dadurch begründen, dass jedes äußere Dreieck jeweils zum inneren Dreieck nach SWS kongruent ist. Wegen der Transitivität der Relation Dreieckskongruenz sind jetzt die äußeren Dreiecke jetzt auch zueinander kongruent. |
| + | |||
| + | Alles in allem aber eine schöne Lösung. | ||
| + | |||
| + | Die Konstellation hier noch mal zum dynamischen Verändern: | ||
| + | |||
| + | <ggb_applet width="523" height="339" version="4.2" ggbBase64="UEsDBBQACAgIAMFUP0IAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAMFUP0IAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vvbctu2Fn1OvwLDZ4siQIKXjJSOr9N03DZT55w5c95AEpJYUyRLUpbcyef0B3q/vp33fNPZAEiJ1CUKZdfjZGxHBkHittfaWHuDdgafLqYxuuF5EaXJUMO6oSGeBGkYJeOhNitHPVf79MUngzFPx9zPGRql+ZSVQ83SibbqBzUdu6JzFA41QqjvuTTo2a7Fe5brOD3PdEc9YjPXCy2T2P5IQ2hRRM+T9Es25UXGAn4VTPiUXaYBK+WYk7LMnvf78/lcr2fX03zcH499fVGEGoKVJ8VQqy6ew3CtTnNTNieGgfv/+eJSDd+LkqJkScA1JKyaRS8+eTaYR0mYztE8CsvJUKMUzJjwaDwRZjq2hvqiUQa2ZjwooxteQNdGVdpcTjNNNmOJeP5MXaF4aY6GwugmCnk+1AzdtNvfVENpHvGkrBrjatJ+PdzgJuJzNa64klNahucAB1ER+TEfaiMWF2BWlIxygBRWlM+gWpS3MfdZXtdXC8JH8A0Nou+4GAuMVjgAf55xRLBz5BjGkUSjvzaxhso0jeWoBqIeevMGEYMY6EgUWBUECttWjwx1zzBVQVRhqYKqNpbqbqmmlmpjqTaW+Q47q/rK0OpGy9LaTrNpJwb7xMeGjwRgzU63YScWRrxBWKxeFiYS68Zy/aKwqqqtqo4ssKEKXD10xQ+Jl31Hi8yDLMKNWZU/7J50w1/qGSkx339Gcic7l1aSbVYSusPKO4JbT4ppY1KYS/6Tn40pzU527oS2w4y2dZe9f8CEjvEQEw76tdINqr2HioloW7lryaeFUB3Tk8KDMKKwMW0HdIIi7EHhiA1KEKbIolDFLrJF6SBT7EkLmchFoh02kZQX6sIPS+5XG1EYS9x01MZFpoWoibAUJQuBFCEpbCByxIQWlCIKncTsWExr2siyoWK6yIIFCklzhGyY0A/qMDlBJkam6IsdRGxkE+QIWcSWUEvbFWuHQQmyDWSLrqCLoIlKD6GHi0xhDXh4lhbREtwJj7MlKxLHKMlmZQu7YBrWl2W61jpMg+uTNaw5K8r6GhpBMFrFPBWcWiHx2SBmPo8hcbgSboDQDYvFDpbjj9KkRLULEHVvnLNsEgXFFS9L6FWgb9gNu2QlX1xA66JeoJxaRuoBnwVxFEYs+Tf4iBhCDIiWgVvoUh24TYzVLEGa5uHVbQGOgxb/5Xk61HqQqTS/CITfW/UI2+1HVChQwITLW57uNb8gOtxWj6ixNqCamt8sTWMLvjQIjXOxnxqVl8VJGq9uZWmUlKcsK2e5TMNgDbmw6jgZx1yCK3UVEprg2k8XVwpVU431+jaDmqFW4I9P0zjNEexIQsHKcVX6qpRtxNKWrQzZxpAtjJqmKFw+xx6RLWTpq1K2At7V0ipTcW0mNuppokLqCAyuvKwWXuE1Ij+aJVF5WVfKKLiuTMWqw5ezqQ8OV3lke0x8X2MO+ms+NrjmecJj5UkJkDlLZ4Vy7aV7PhvMCv6KlZPjJPyaj2FPvmJCFksYWjVdLTnkQTSFjup+BR4TxP4Llqruhnyc89rEWGa+Clr51Gj69cZtOdRFnk5fJjevwWvWljro1/YMiiCPMuGdyAedvuYr/wujgoHKh81+YHwBVgRCcQDIUoCoITYrJ2kuk1vYt2LXoc//932S8BykEjxS7NmYTyGxRaX0S+naS36OZcosiECp/w0oyTJwqOcr2ODxVh+V3szibMJEWl1hELNbWEATFTneF2m4jhVQIQ0CdciUU2ScK39S64WLDIaT27DBtwS/QAtYgC52wi2IiqkTkITv1CFKHRmEsWJ3tqRQ3V0jDvxO4bQHsZMPHzFb96waMdP+xxE7/fARo3C2VohhnVj3gliQTqcsCVEis7dXaXw7ThNtlTcwQ+xOxLBwOcSIwFGBNCvr5yCQMUQgrJoFqhmDwhxqvpqwmmYLRWrCmoTlUO1QUkJ6cA0H4ELGu7KKbPLisygMucx9+u/mt4Fok2AsIjsATnEV61YM4y4M73bDgo9FbbmQYI8jdl9oR1dcORR0dVsJi+FI/7J0OMW30h/lbCBylGzmN4cQBf4TC1d/mYjoyGU82Yyn15xnIpH5Knmds6QQL53agfT9YWePB/Ye0TGpN7JjrxMASLu643l4lWM6HxDQ/uMBmuhGFWKITlSI6WERbTzazN8fE7ZtQb6ERa2p8Wkts+syHL5baoV9Sw7CwzhqnwoeXoAsnTrA6MF88W8T1aVQ2X80zeIoiMrOJJwoEvwNEngHEvgjIWHbLiEgTBTfjwLdG+pVIsI2UB91QH30SFDfHwQM3cJOU6ge3POXurZGxEgREW4QcbYv3Wtm5GcHZeS2K5kQha+Ku3Ph6Q4hNqUrZ5e8VLftKiSbLrbvMdneBS5X4I42wD3vAu75owHX9HRCqOvWQo8VuBYFsTFsqwHuRmL5EDhvOvFFF5wvHg3OjqNjbDi1psDJ0DYdTFaQ/iNeLN9Fbo+Op+okeLEB8Nsf3o2wfHe1RBBai/6wmFm9JN2lroFdD5uWZXrUogce/nad7vF7s1CfEbtIcv2yLw8a4NevCeI4nX/NRzFfSGTfN1HcRsNp69x+vEnDj51o+HEvDfYTDVtoOGvthi00/NSJhp82aXAoJAqOiym1sYfrBLkzDYQoIohiwjY+MiIqWTre9R7r7c+diPj5iYgDiajy+LOdRPzSiYhf9gqT+yRMu+PDhaLhZJOGXzvR8Ove/XBomP7Y98PFnhfsb3/rRMRv60RgnRIP9oFHLOqaHjl0O6z/6hiLpPKjYqIKEec7Y/XvnZj4fS8TT1TsCRKnO9Xpj05U/LGXikN/g/TxU3HaSpzONqn4sxMVfz7p06FMnLeY2LIp/urExF9PJ+u7aFMVsM83afi7Ew1/78mcDM978Mzpq9Go4KV8f0erv9JwHxlP/ebfIsk/Dqz+e8CL/wNQSwcIPT6HK5MIAADOMAAAUEsBAhQAFAAICAgAwVQ/QtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADBVD9CPT6HK5MIAADOMAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAACoJAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Version vom 31. Januar 2013, 10:38 Uhr
Aufgabe 12.06Beweisen Sie: Die Höhen eines Dreiecks (bzw. die Geraden, die durch die Höhen eindeutig bestimmt sind) schneiden einander in genau einem Punkt.
Lösung User Caro44--Caro44 13:53, 30. Jan. 2013 (CET) Lösung User B.....
Bemerkungen --*m.g.* 09:48, 31. Jan. 2013 (CET)
Alles in allem aber eine schöne Lösung. Die Konstellation hier noch mal zum dynamischen Verändern:
|
 ein Dreieck. Von diesem Dreieck wissen Sie bereits, dass sich seine Mittelsenkrechten in genau einem Punkt schneiden. Konstruieren aus
ein Dreieck. Von diesem Dreieck wissen Sie bereits, dass sich seine Mittelsenkrechten in genau einem Punkt schneiden. Konstruieren aus 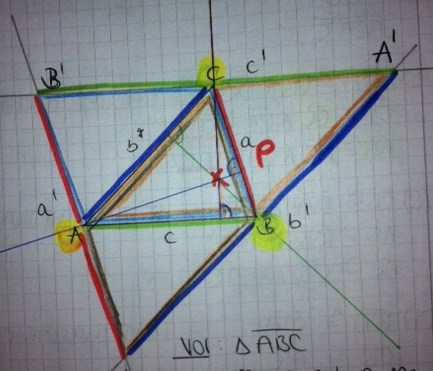


 außerhalb einer Geraden
außerhalb einer Geraden  geht eine zu
geht eine zu  . Was wir nicht beweisen können und deshalb axiomatisch fordern, ist die Tatsache, dass es höchstens eine solche Gerade geben kann.
. Was wir nicht beweisen können und deshalb axiomatisch fordern, ist die Tatsache, dass es höchstens eine solche Gerade geben kann.

