Probeklausur WS 12 13 Aufgabe 1: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe d) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 23: | Zeile 23: | ||
=Aufgabe d= | =Aufgabe d= | ||
Nur unter Verwendung der Eigenschaft <math>E_1</math> sei der Begriff <math>B</math> korrekt definiert. Es stellt sich heraus, dass <math>B</math> ebenso korrekt über die Eigenschaft <math>E_2</math> hätte definiert werden können.<br /> Was ist <math>E_1</math> hinsichtlich einer Entscheidung, ob ein Repräsentant <math>R</math> zum Begriff <math>B</math> gehört? | Nur unter Verwendung der Eigenschaft <math>E_1</math> sei der Begriff <math>B</math> korrekt definiert. Es stellt sich heraus, dass <math>B</math> ebenso korrekt über die Eigenschaft <math>E_2</math> hätte definiert werden können.<br /> Was ist <math>E_1</math> hinsichtlich einer Entscheidung, ob ein Repräsentant <math>R</math> zum Begriff <math>B</math> gehört? | ||
| + | |||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | =Aufgabe e= | ||
| + | |||
| + | Es sei <math>R</math> ein beliebiger Punkt und <math>r \in \mathbb{R}, r>0</math> Was ist das? <math>M:=\left\{P||RP|\leq r \right\}</math>. | ||
| + | |||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | =Aufgabe f= | ||
Version vom 3. Februar 2013, 17:45 Uhr
Inhaltsverzeichnis |
Aufgabe a
Es seien 
und 
zwei verschiedene Punkte.
Ergänzen Sie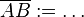 
.
Lösung User ...
Lösung User ...
Aufgabe b
Definieren Sie den Begriff komplanar für die Anzahl von Punkten, ab der der Begriff sinnvoll ist.
Lösung User ...
Lösung User ...
Aufgabe c
Definieren Sie den Begriff Raute unter Verwendung des Oberbegriffs Viereck.
Lösung User ...
Lösung User ...
Aufgabe d
Nur unter Verwendung der Eigenschaft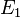 
sei der Begriff korrekt definiert. Es stellt sich heraus, dass ebenso korrekt über die Eigenschaft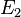 
hätte definiert werden können.
Was ist 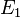hinsichtlich einer Entscheidung, ob ein Repräsentant 
zum Begriff gehört?
Lösung User ...
Lösung User ...
Aufgabe e
Es sei ein beliebiger Punkt und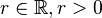 
Was ist das? 
.
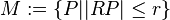