Probeklausur WS 12 13 Aufgabe 4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe a) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe a) |
||
| Zeile 14: | Zeile 14: | ||
Für den folgenden Beweis beziehen wir uns auf Abb. 03. Hier wurde der Durchmesser <math>\overline{CD}</math> eingezeichnet und zum Viereck <math>\overline{ACBD}</math> ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment: | Für den folgenden Beweis beziehen wir uns auf Abb. 03. Hier wurde der Durchmesser <math>\overline{CD}</math> eingezeichnet und zum Viereck <math>\overline{ACBD}</math> ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment: | ||
| − | + | ==Lösung User ...== | |
{| class="wikitable" | {| class="wikitable" | ||
!Nr.!!Beweisschritt!!Begründung | !Nr.!!Beweisschritt!!Begründung | ||
| Zeile 34: | Zeile 34: | ||
|(VII)|| <math>2\cdot\left(|\gamma_1|+|\gamma_2| \right)=180</math>° || ... | |(VII)|| <math>2\cdot\left(|\gamma_1|+|\gamma_2| \right)=180</math>° || ... | ||
|} | |} | ||
| + | ==Lösung User ...== | ||
| + | {| class="wikitable" | ||
| + | !Nr.!!Beweisschritt!!Begründung | ||
| + | |- | ||
| + | | (I) || <math>\overline{MC} \tilde= \overline{MA} \tilde= \overline{MD} \tilde= \overline{MB}</math> || ... | ||
| + | |- | ||
| + | | (II) ||<math>|\gamma_1|+|\gamma_2| + |\delta_1| + |\delta_2|=180</math>° || ... | ||
| + | |- | ||
| + | | (III) || <math>\varphi_1 \tilde=\varphi_2 \wedge \varepsilon_1 \tilde= \varepsilon_2</math> || ... | ||
| + | |- | ||
| + | | (IV) || <math>\overline{AMC} \tilde= \overline{BMD} \wedge \overline{BMC} \tilde=\overline{AMD}</math> || ... | ||
| + | |- | ||
| + | |(V)|| <math>\delta_1 \tilde= \gamma_1 \wedge \delta_2 \tilde= \gamma_2</math> || ... | ||
| + | |- | ||
| + | |(VI)||<math> |\gamma_1|+|\gamma_2| + |\gamma_1| + |\gamma_2|=180</math>° || ... | ||
| + | |- | ||
| + | |(VIII)|| <math>|\gamma_1|+|\gamma_2| = |\gamma|=90</math>° || ... | ||
| + | |- | ||
| + | |(VII)|| <math>2\cdot\left(|\gamma_1|+|\gamma_2| \right)=180</math>° || ... | ||
| + | |} | ||
| + | =Aufgabe b= | ||
| + | Formulieren Sie den unter a) bewiesenen Satz in allgemeinerer Form unter Verwendung der Begriffe Dreieck und Umkreis in der Form Wenn-Dann. | ||
| + | |||
| + | ==Lösung User ...== | ||
| + | |||
| + | |||
| + | ==Lösung User ...== | ||
Version vom 3. Februar 2013, 18:50 Uhr
 |
|
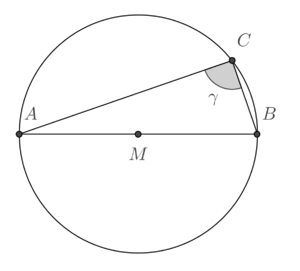
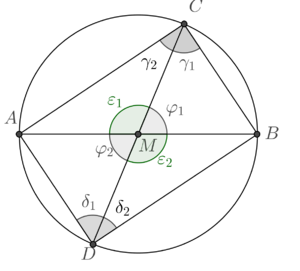
| Abbildung 02 | Abbildungs 03 |
Inhaltsverzeichnis |
Aufgabe a
Es sei 
ein Kreis mit dem Mittelpunkt 
, auf seien drei nichtkollineare Punkte 
gegeben.
Voraussetzung 1: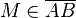 
,
Voraussetzung 2: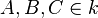 
,
Behauptung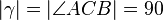 
°
Für den folgenden Beweis beziehen wir uns auf Abb. 03. Hier wurde der Durchmesser 
eingezeichnet und zum Viereck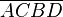 
ergänzt. Die Korrektheit dieser Konstruktion muss nicht begründet werden. Ergänzen Sie das folgende Beweisfragment:
Lösung User ...
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) |  |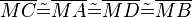
... |
| (II) |  ° |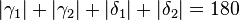
... |
| (III) |  |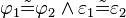
... |
| (IV) |  |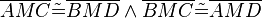
... |
| (V) |  |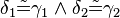
... |
| (VI) |  ° |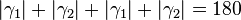
... |
| (VIII) |  ° |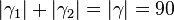
... |
| (VII) |  ° |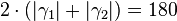
... |
Lösung User ...
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | |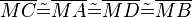
... |
| (II) | ° |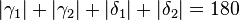
... |
| (III) | |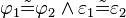
... |
| (IV) | |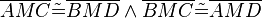
... |
| (V) | |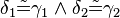
... |
| (VI) | ° |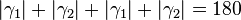
... |
| (VIII) | ° |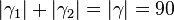
... |
| (VII) | ° |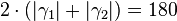
... |
Aufgabe b
Formulieren Sie den unter a) bewiesenen Satz in allgemeinerer Form unter Verwendung der Begriffe Dreieck und Umkreis in der Form Wenn-Dann.
