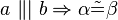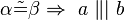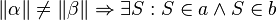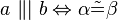Lösung von Aufgabe 3.3 (WS 12 13 P): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine…“) |
|||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
#<math>\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b </math> | #<math>\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b </math> | ||
#<math>\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta </math> | #<math>\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta </math> | ||
| + | |||
| + | zu a) Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander. --[[Benutzer:Der Bohrer|Der Bohrer]] 11:16, 22. Nov. 2012 (CET) | ||
| + | |||
| + | Zu b) | ||
| + | |||
| + | 1. Stufenwinkelsatz | ||
| + | * korrekt--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:44, 4. Feb. 2013 (CET) | ||
| + | |||
| + | 2. Umkehrung Stufenwinkelsatz | ||
| + | * korrekt--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:44, 4. Feb. 2013 (CET) | ||
| + | |||
| + | 3. Die Geraden wären identisch somit trotzdem paralell und somit existieren die Winkel nicht, beziehungsweise es wären Nebenwinkel. | ||
| + | * Die Geraden könnten auch einfach einen Schnittpunkt haben, es steht ja nirgens, dass sie parallel sind. Das ist also nicht die richtige Begründung.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:44, 4. Feb. 2013 (CET) | ||
| + | 4. Äquivalentsaussage des Stufenwinkelsatzes<br /> | ||
| + | --Würmli 13:30, 3. Feb. 2013 (CET | ||
| + | * Das ist eine Äquivalenzaussage - richtig. Aber sie ist nicht äquivalent zum Stufenwinkelsatz.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:44, 4. Feb. 2013 (CET) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 4. Februar 2013, 12:44 Uhr
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel 
und 
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
zu a) Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander. --Der Bohrer 11:16, 22. Nov. 2012 (CET)
Zu b)
1. Stufenwinkelsatz
- korrekt--Tutorin Anne 12:44, 4. Feb. 2013 (CET)
2. Umkehrung Stufenwinkelsatz
- korrekt--Tutorin Anne 12:44, 4. Feb. 2013 (CET)
3. Die Geraden wären identisch somit trotzdem paralell und somit existieren die Winkel nicht, beziehungsweise es wären Nebenwinkel.
- Die Geraden könnten auch einfach einen Schnittpunkt haben, es steht ja nirgens, dass sie parallel sind. Das ist also nicht die richtige Begründung.--Tutorin Anne 12:44, 4. Feb. 2013 (CET)
4. Äquivalentsaussage des Stufenwinkelsatzes
--Würmli 13:30, 3. Feb. 2013 (CET
- Das ist eine Äquivalenzaussage - richtig. Aber sie ist nicht äquivalent zum Stufenwinkelsatz.--Tutorin Anne 12:44, 4. Feb. 2013 (CET)
