Lösung von Aufg. 6.4P (WS 12/13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Würmli (Diskussion | Beiträge) |
|||
| Zeile 14: | Zeile 14: | ||
!Beweisschritt!!Begründung | !Beweisschritt!!Begründung | ||
|- | |- | ||
| − | | 1 | + | | 1 A <math>\in</math> M, B <math>\in</math> M <math>\Rightarrow</math> <math>\overline{AB} \in</math> M || Weil M konvex ist |
|- | |- | ||
| − | | 2 | + | | 2 A <math>\in</math> N, B <math>\in</math> N <math>\Rightarrow</math> <math>\overline{AB} \in</math> N || Weil N konvex ist |
|- | |- | ||
| 3 (Schritt) || (Begründung) | | 3 (Schritt) || (Begründung) | ||
| Zeile 23: | Zeile 23: | ||
|} | |} | ||
<br /> | <br /> | ||
| + | |||
| + | --Würmli 13:09, 4. Feb. 2013 (CET) | ||
| + | |||
Habe mal den Anfang gemacht. Wer macht ein Stück weiter? Nicht (ganz) korrekte Beweise sind übrigens wesentlich lehrricher als richtige Beweise - das ist ja keine neue Weisheit.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:59, 10. Dez. 2012 (CET) | Habe mal den Anfang gemacht. Wer macht ein Stück weiter? Nicht (ganz) korrekte Beweise sind übrigens wesentlich lehrricher als richtige Beweise - das ist ja keine neue Weisheit.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:59, 10. Dez. 2012 (CET) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 4. Februar 2013, 13:09 Uhr
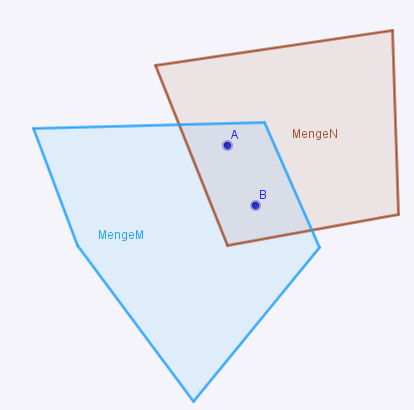
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
| Voraussetzung | M und N sind konvex--Der Bohrer 14:08, 13. Dez. 2012 (CET) |
| Behauptung | Schnittmenge ist konvex--Der Bohrer 14:08, 13. Dez. 2012 (CET) |
| Beweisschritt | Begründung |
|---|---|
1 A  M, B M, B  M M  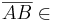 M M |
Weil M konvex ist |
2 A  N, B N, B  N N  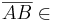 N N |
Weil N konvex ist |
| 3 (Schritt) | (Begründung) |
| 4 (Schritt) | (Begründung) |
--Würmli 13:09, 4. Feb. 2013 (CET)
Habe mal den Anfang gemacht. Wer macht ein Stück weiter? Nicht (ganz) korrekte Beweise sind übrigens wesentlich lehrricher als richtige Beweise - das ist ja keine neue Weisheit.--Tutorin Anne 12:59, 10. Dez. 2012 (CET)