Lösung von Aufg. 6.4P (WS 12/13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Würmli (Diskussion | Beiträge) |
Würmli (Diskussion | Beiträge) |
||
| Zeile 18: | Zeile 18: | ||
| 2 A <math>\in</math> N, B <math>\in</math> N <math>\Rightarrow</math> <math>\overline{AB} \in</math> N || Weil N konvex ist | | 2 A <math>\in</math> N, B <math>\in</math> N <math>\Rightarrow</math> <math>\overline{AB} \in</math> N || Weil N konvex ist | ||
|- | |- | ||
| − | | 3 | + | | 3 <math>\ M \cap N</math> <math>\Rightarrow</math> <math>A \in \ M \wedge N, B \in \ M \wedge N,</math> || 1), 2) |
|- | |- | ||
| − | | 4 | + | | 4 <math>\overline{AB} \in \ M \wedge N</math> || 3) |
|} | |} | ||
<br /> | <br /> | ||
| + | Weil <math>\overline{AB}</math> Element der Schnittmenge ist. Ist die Schnittmenge konvex. Somit ist die Behauptung korrekt. | ||
| + | Geht das mit dem und Zeichen oder muss ich das für jede Menge extra machen? | ||
--Würmli 13:09, 4. Feb. 2013 (CET) | --Würmli 13:09, 4. Feb. 2013 (CET) | ||
Version vom 4. Februar 2013, 15:53 Uhr
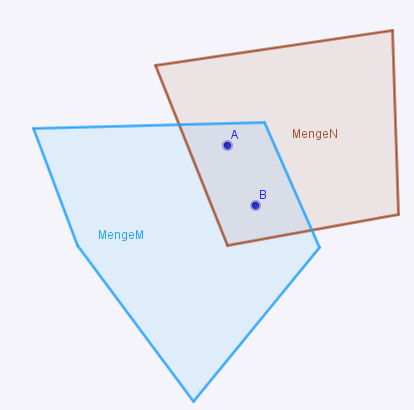
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
| Voraussetzung | M und N sind konvex--Der Bohrer 14:08, 13. Dez. 2012 (CET) |
| Behauptung | Schnittmenge ist konvex--Der Bohrer 14:08, 13. Dez. 2012 (CET) |
| Beweisschritt | Begründung |
|---|---|
1 A  M, B M, B  M M  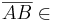 M M |
Weil M konvex ist |
2 A  N, B N, B  N N  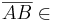 N N |
Weil N konvex ist |
3 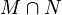  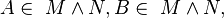 |
1), 2) |
4 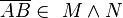 |
3) |
Weil  Element der Schnittmenge ist. Ist die Schnittmenge konvex. Somit ist die Behauptung korrekt.
Element der Schnittmenge ist. Ist die Schnittmenge konvex. Somit ist die Behauptung korrekt.
Geht das mit dem und Zeichen oder muss ich das für jede Menge extra machen? --Würmli 13:09, 4. Feb. 2013 (CET)
Habe mal den Anfang gemacht. Wer macht ein Stück weiter? Nicht (ganz) korrekte Beweise sind übrigens wesentlich lehrricher als richtige Beweise - das ist ja keine neue Weisheit.--Tutorin Anne 12:59, 10. Dez. 2012 (CET)