Lösung von Aufgabe 12.4P (WS 12 13): Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | ||
<br /> | <br /> | ||
| − | [[Datei:TobiWan_Beweis1.jpg | | + | [[Datei:TobiWan_Beweis1.jpg | 1000px]] |
<br />--[[Benutzer:TobiWan|TobiWan]] 23:51, 30. Jan. 2013 (CET)<br /><br /> | <br />--[[Benutzer:TobiWan|TobiWan]] 23:51, 30. Jan. 2013 (CET)<br /><br /> | ||
Gute Konstruktion mit Erklärung dazu - danke! Das Drehzentrum wäre damit gefunden. Wenn es heißt "zeigen Sie" muss du zudem aber begründen, dass es immer bei einer Drehung verkettet mit einer Verschiebung zu einer Drehung kommt. Das kann nicht anhand einer Zeichnung gemacht werden, sondern muss allgemein (über die Lage der Spiegelachsen) erklärt werden.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:23, 31. Jan. 2013 (CET) | Gute Konstruktion mit Erklärung dazu - danke! Das Drehzentrum wäre damit gefunden. Wenn es heißt "zeigen Sie" muss du zudem aber begründen, dass es immer bei einer Drehung verkettet mit einer Verschiebung zu einer Drehung kommt. Das kann nicht anhand einer Zeichnung gemacht werden, sondern muss allgemein (über die Lage der Spiegelachsen) erklärt werden.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:23, 31. Jan. 2013 (CET) | ||
| + | <br /> | ||
| + | [[Datei:TobiWan_Drehungverschiebungdrehung.jpg | 1000px]] | ||
| + | <br />--[[Benutzer:TobiWan|TobiWan]] 20:58, 1. Feb. 2013 (CET)<br /> | ||
| + | Gute Idee! Du bist auf dem richtigen Weg.<br /> | ||
| + | Wichtig ist, dass du die Reihenfolge der Geradenspiegelungen nicht vertauscht, denn sie ist ja für den Drehwinkel und die Verschiebungsrichtung entscheidend. Weshalb sollte man Gerade a und c' reduzieren dürfen - kannst du das begründen?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:13, 2. Feb. 2013 (CET)<br /><br /> | ||
| + | <br /> | ||
| + | Versuch 2:<br /> | ||
| + | [[Datei:TobiWan_001.jpg | 800px]]<br />--[[Benutzer:TobiWan|TobiWan]] 20:32, 2. Feb. 2013 (CET)<br /><br />Sehr gute Zeichnung!Auch die Erklärung ist gut. Zu Ergänzen ist noch eine Begründung, warum der Winkel der neuen Drehung mit der Orginaldrehung übereinstimmt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:36, 4. Feb. 2013 (CET)<br /><br /> | ||
| + | Wenn b' parallel d', dann gilt der Stufenwinkelsatz.Daraus folgt dann, dass der Winkel der neuen Drehung mit dem Originalwinkel übereinstimmt.--[[Benutzer:TobiWan|TobiWan]] 19:39, 4. Feb. 2013 (CET)<br /><br /> | ||
| + | *Sehr gut!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:30, 5. Feb. 2013 (CET) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 5. Februar 2013, 17:30 Uhr
Zeigen Sie, dass die Verkettung einer Drehung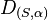 
mit einer Verschiebung wieder eine Drehung 
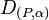ergibt. Wo liegt das neue Drehzentrum P?
--TobiWan 23:51, 30. Jan. 2013 (CET)
Gute Konstruktion mit Erklärung dazu - danke! Das Drehzentrum wäre damit gefunden. Wenn es heißt "zeigen Sie" muss du zudem aber begründen, dass es immer bei einer Drehung verkettet mit einer Verschiebung zu einer Drehung kommt. Das kann nicht anhand einer Zeichnung gemacht werden, sondern muss allgemein (über die Lage der Spiegelachsen) erklärt werden.--Tutorin Anne 17:23, 31. Jan. 2013 (CET)
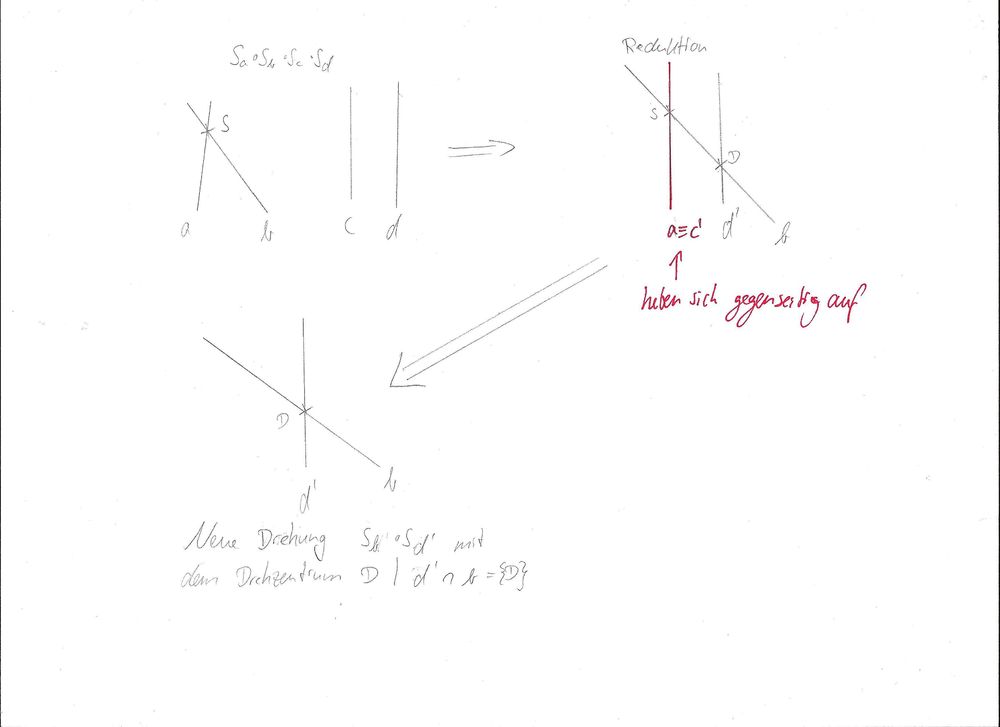
--TobiWan 20:58, 1. Feb. 2013 (CET)
Gute Idee! Du bist auf dem richtigen Weg.
Wichtig ist, dass du die Reihenfolge der Geradenspiegelungen nicht vertauscht, denn sie ist ja für den Drehwinkel und die Verschiebungsrichtung entscheidend. Weshalb sollte man Gerade a und c' reduzieren dürfen - kannst du das begründen?--Tutorin Anne 15:13, 2. Feb. 2013 (CET)
Versuch 2:
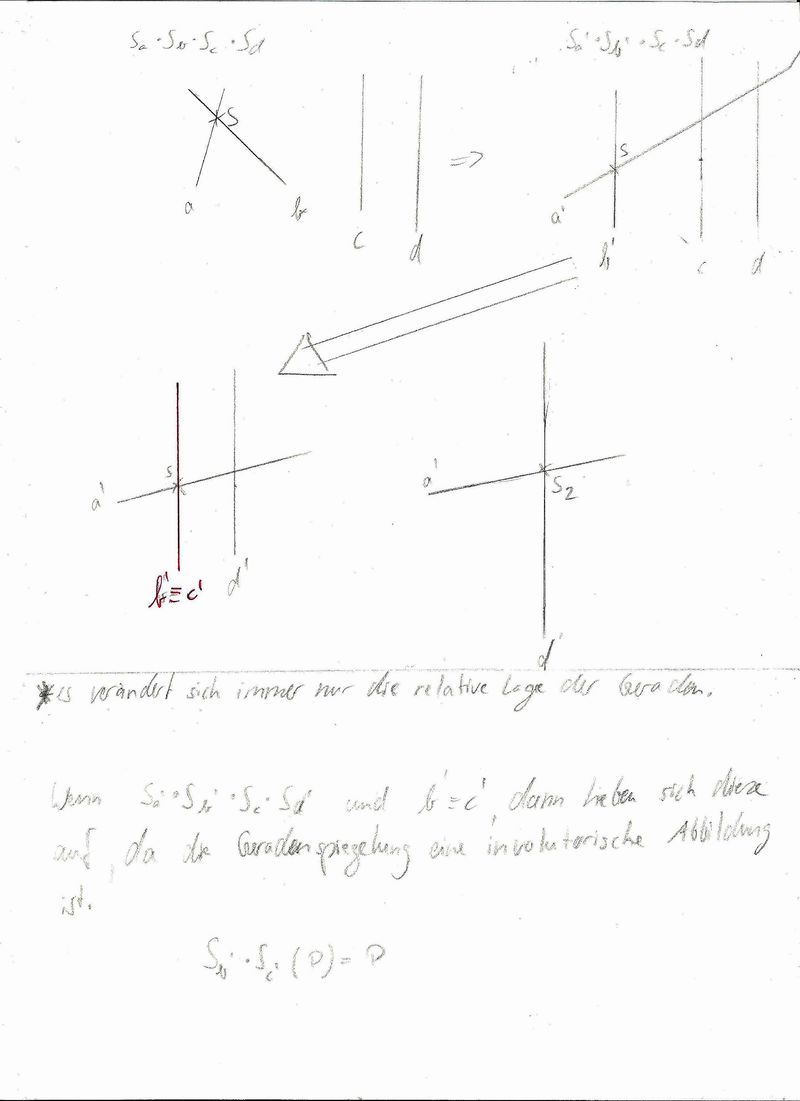
--TobiWan 20:32, 2. Feb. 2013 (CET)
Sehr gute Zeichnung!Auch die Erklärung ist gut. Zu Ergänzen ist noch eine Begründung, warum der Winkel der neuen Drehung mit der Orginaldrehung übereinstimmt.--Tutorin Anne 12:36, 4. Feb. 2013 (CET)
Wenn b' parallel d', dann gilt der Stufenwinkelsatz.Daraus folgt dann, dass der Winkel der neuen Drehung mit dem Originalwinkel übereinstimmt.--TobiWan 19:39, 4. Feb. 2013 (CET)
- Sehr gut!--Tutorin Anne 17:30, 5. Feb. 2013 (CET)
