Probeklausur WS 12 13 Aufgabe 1: Unterschied zwischen den Versionen
(→Lösung User Ron) |
B..... (Diskussion | Beiträge) (→Lösung User Ron) |
||
| Zeile 59: | Zeile 59: | ||
==Lösung User Ron== | ==Lösung User Ron== | ||
| − | Ein Kriterium | + | Ein Kriterium<br /> |
| + | <br /> Frage dazu: Wenn es ein Kriterium ist, kann man dann auch sagen, dass es notwendig und hinreichend ist?--[[Benutzer:B.....|B.....]] 20:20, 5. Feb. 2013 (CET) | ||
===Bewertung=== | ===Bewertung=== | ||
2 von 2 Punkten | 2 von 2 Punkten | ||
| − | |||
==Lösung User --[[Benutzer:Sweetnightmare5|Sweetnightmare5]] 19:27, 5. Feb. 2013 (CET)== | ==Lösung User --[[Benutzer:Sweetnightmare5|Sweetnightmare5]] 19:27, 5. Feb. 2013 (CET)== | ||
Version vom 5. Februar 2013, 20:20 Uhr
|
Aufgabe aEs seien Lösung User Ron{P/ Zw (A,P,B)} U {A,B} Bewertung2 von 2 Punkten Lösung User ...Aufgabe bDefinieren Sie den Begriff komplanar für die Anzahl von Punkten, ab der der Begriff sinnvoll ist. Lösung User ...Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Bewertung1 von 2 Punkten --*m.g.* 18:01, 4. Feb. 2013 (CET) Vier Punkte heißen komplanar, wenn sie in ein und derselben Ebene liegen.--Caro44 20:01, 4. Feb. 2013 (CET) Vier Punkte A, B, C, und D sind komplanar, wenn es eine Ebene gibt, die alle diese Punkte enthält. --...lw)... 10:45, 5. Feb. 2013 (CET) Lösung User ...
Aufgabe cDefinieren Sie den Begriff Raute unter Verwendung des Oberbegriffs Viereck. Lösung User RonEin Viereck ist eine Raute, wenn alle vier Seiten gleich lang sind. Bewertung2 von 2 Punkten--*m.g.* 18:02, 4. Feb. 2013 (CET) Lösung ...lw)...Eine Raute ist ein Viereck mit zwei Paar paralleler und 3 gleichlangen Seiten. --...lw)... 10:46, 5. Feb. 2013 (CET) Lösung User RonWenn ein Viereck eine Raute ist, dann sind alle vier Seiten des Vierecks gleich lang. Bewertung0 von 2 Punkten--*m.g.* 18:03, 4. Feb. 2013 (CET) Aufgabe dNur unter Verwendung der Eigenschaft
Lösung User RonEin Kriterium Bewertung2 von 2 Punkten Lösung User --Sweetnightmare5 19:27, 5. Feb. 2013 (CET)Hinreichende Bedingung Bewertung? von 2 Punkten Lösung User ...Aufgabe eEs sei
Lösung User ...Eine Kugel Bewertung1 von 2 Punkten--*m.g.* 18:04, 4. Feb. 2013 (CET) Lösung User AaliyahEs ist eine Kugel um P mit dem Radius r inklusive ihres Inneren.--Aaliyah 18:55, 4. Feb. 2013 (CET)
Lösung User ...lw)...M ist eine Kugel mit dem Radius RP. --...lw)... 10:50, 5. Feb. 2013 (CET) Aufgabe fDefinieren Sie den Begriff Rechter Winkel wie in der Vorlesung.
Lösung User RonEin Winkel, der so groß ist, wie einer seiner Nebenwinkel, nennt man rechter Winkel. Bewertung2 von 2 Punkten mit sehr großen Bauchschmerzen: Lösung User AaliyahWenn ein Winkel so groß ist, wie einer seiner Nebenwinkel, dann ist der Winkel ein Rechter.--Aaliyah 18:57, 4. Feb. 2013 (CET) Aufgabe gErgänzen Sie die folgende Definition: Zwei Geraden
Lösung User Ron,wenn sie nicht parallel sind und keinen gemeinsamen Schnittpunkt(schnittfrei sind) haben Bewertung2 von 2 Punkten, besser schnittpunktfrei --*m.g.* 18:08, 4. Feb. 2013 (CET) Lösung User ...Aufgabe hDefinieren Sie den Begriff Tangentialebene einer Kugel.
Lösung User RonEine Ebene, welche eine Kugel in einem Punkt berührt, nennt man Tangentialebene Bewertung1 von 2 Punkten--*m.g.* 18:10, 4. Feb. 2013 (CET) Lösung User AaliyahEs sei k eine Kugel. Eine Ebene E, die mit der Kugel k genau einen Berührpunkt B hat, nennt man Tangentialebene an der Kugel k.--Aaliyah 19:00, 4. Feb. 2013 (CET)
|
 und
und  zwei verschiedene Punkte.
zwei verschiedene Punkte.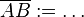 .
.
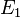 sei der Begriff
sei der Begriff 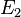 hätte definiert werden können.
hätte definiert werden können. zum Begriff
zum Begriff 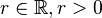 . Was ist das?
. Was ist das? 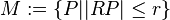 .
.
 und
und  sind windschief, wenn
sind windschief, wenn 

