Definitionen in der Mathematik SoSe 13 S: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Was sind mathematische Definitionen?) |
*m.g.* (Diskussion | Beiträge) (→Was sind mathematische Definitionen?) |
||
| Zeile 27: | Zeile 27: | ||
== Was sind mathematische Definitionen? == | == Was sind mathematische Definitionen? == | ||
| + | ===Ein Quiz=== | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{ Bei welchen der folgenden "Definitionen" würde einem echten Mathematiker unwohl sein?} | { Bei welchen der folgenden "Definitionen" würde einem echten Mathematiker unwohl sein?} | ||
| Zeile 40: | Zeile 41: | ||
||wiederum vorausgesetzt geordnetes Tripel, natürliche Zahl etc. wurde bereits definiert. | ||wiederum vorausgesetzt geordnetes Tripel, natürliche Zahl etc. wurde bereits definiert. | ||
</quiz> | </quiz> | ||
| + | ===Fazit=== | ||
| + | Will man eine Begriffsbeschreibung effizient erstellen, so wird man sinnvollerweise auf andere Begriffe zurückgreifen. All diese Begriffe müssen ihrerseits vorab festgelegt worden sein. | ||
| + | |||
| + | ===undefinierte Grundbegriffe=== | ||
| + | |||
| + | * Ein Quadrat ist eine Rechteck mit ... | ||
| + | * Ein Rechteck ist ein Parallelogramm mit ... | ||
| + | * Ein Parallelogramm ist ein Trapez mit ... | ||
| + | * Ein Trapez ist ein Viereck mit ... | ||
| + | * Eine Viereck ist die Vereingungsmenge von vier Strecken, wobei ... | ||
| + | * Die Strecke <math>\overline{AB}</math> ist die Menge aller Punkte, die zwischen den Punkten <math>A</math> und <math>B</math> liegt vereinigt mit der Menge, die aus den Punkten <math>A</math> und <math>B</math> besteht. | ||
| + | * Ein Punkt ist ...? | ||
| + | Irgendwann sind wir mit der Rückführung auf andere Begriffe am Ende. Wir müssen akzeptieren, dass wir nicht alles sauber und exakt definieren können, obwohl wir doch sehr genaue Vorstellungen von unserem Begriff haben. Der Mathematiker geht dann von sogenannten undefinierten Grundbegriffen aus: | ||
| + | |||
| + | * Punkt | ||
| + | * Gerade | ||
| + | * Ebene | ||
| + | |||
| + | Wir ergänzen: | ||
| + | |||
| + | Eine mathematische Definition ist eine Begriffsbeschreibung, die nur bereits definierte Begriffe bzw. als undefiniert festgelegte Grundbegriffe verwendet. | ||
=Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulieren= | =Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulieren= | ||
Version vom 18. April 2013, 21:34 Uhr
|
Aufgaben vorabDefinieren Sie:
Was ist eine Definition?Rein aus der Intuition herausZuordnung passt zum Begriff Definition passt nicht zum Begriff Definition ist eine GesetzmäßigkeitFestlegungwird durch den Menschen geschaffenNaturgesetzist entweder wahr oder falschexistiert unabhängig vom menschlichen Bewußtseinjuristisches Gesetzmathematische AussageBegriffsbeschreibungist weder wahr noch falschFalls es Gott geben sollte so hat er sie erschaffenNamensgebung Was ist nun eine DefinitionEs ist schwer den Begriff mathematische Definition sauber zu klären (zu definieren). Wir wollen unter einer Definition die Beschreibung, Festlegung eines Begriffes verstehen. Aus mathematischer Sicht sind an eine derartige Begriffsbeschreibung gewisse Forderungen zu stellen. Was sind mathematische Definitionen?Ein QuizFazitWill man eine Begriffsbeschreibung effizient erstellen, so wird man sinnvollerweise auf andere Begriffe zurückgreifen. All diese Begriffe müssen ihrerseits vorab festgelegt worden sein. undefinierte Grundbegriffe
Irgendwann sind wir mit der Rückführung auf andere Begriffe am Ende. Wir müssen akzeptieren, dass wir nicht alles sauber und exakt definieren können, obwohl wir doch sehr genaue Vorstellungen von unserem Begriff haben. Der Mathematiker geht dann von sogenannten undefinierten Grundbegriffen aus:
Wir ergänzen: Eine mathematische Definition ist eine Begriffsbeschreibung, die nur bereits definierte Begriffe bzw. als undefiniert festgelegte Grundbegriffe verwendet. Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulierenEs gibt verschiedene Arten, Definitionen zu formulieren. Beispiel 1: ggT zweier ganzer ZahlenDie Begriffe Teiler und Euklidischer Algorithmus seien im Folgenden bereits exakt definiert. Das Übliche, die Realdefinition
Konventionaldefinition, das Ganze in "wenn-dann"
Schön, aber wie bekomme ich den ggT: die genetisch, operative Definition
Beispiel 2: DrachenviereckDie Begriffe Dreieck, Viereck, Diagonale, Eckpunkt, Geradenspiegelung und achsensymmetrisch seien im Folgenden bereits definiert. Realdefinition
Konventionaldefinition
genetisch, operative Definition
Ein wenig Didaktik: Definitionen auf verschiedenen NiveaustufenAus didaktischer Sicht lassen sich Definitionen auf verschiedenen Niveaustufen formulieren.
Entwicklung einer "neuen" DefinitionGärtnerkonstruktion der EllipseVideoIm Folgenden wollen wir versuchen, den (ihnen vermutlich wenig geläufigen) Begriff Ellipse zu definieren. Konstruktiv lässt sich eine Ellipse mit Hilfe der sogenannten Gärtnerkonstruktion, wie im folgenden Video, erzeugen. EmbedVideo erhielt die unbrauchbare ID „PQjeTmY0cdQ&NR=1“ für „youtube“.
Bemerkung zu obigem Video: Das geht natürlich noch schöner. Ansporn für Sie? AppletDas folgende Applet empfindet die Gärtnerkonstruktion nach. Aufgaben zur Gärtnerkonstruktion
Vereinbarung: Wir setzen ebene Geometrie voraus. Definition E.1: EllipseAlle Punkte P (mit P liegt in der Ebene E und alle P Element k) für die gilt: Strecke AP + Strecke BP = q (q sei eine feste Zahl).--Natürliches Mineralwasser 15:02, 17. Jan. 2013 (CET) Definition K.1: Kreis als spezielle Ellipse... Zurückführen auf bereits vorhanden Definitionen: Verwenden von OberbegriffenDas Haus der Vierecke
[ www.ph-heidelberg.de is not an authorized iframe site ]
|
mit Mittelpunkt 
und Radius 
ist die Menge aller Punkte, die zwischen den Punkten 
und 
liegt vereinigt mit der Menge, die aus den Punkten 
und 
zwei ganze Zahlen. 
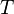sei die Menge aller Zahlen, die sowohl Teiler von 
sowohl die ganze Zahl 
gibt, die auch 
ein Dreieck und 
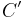das Bild von 
bei der Spiegelung an 
. Das Viereck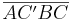 
ist ein Drachenviereck.
