Definitionen in der Mathematik SoSe 13 S: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Exaktheit und Minimalität mathematischer Definitionen) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 1) |
||
| (13 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 83: | Zeile 83: | ||
===Beispiele=== | ===Beispiele=== | ||
====Beispiel 1==== | ====Beispiel 1==== | ||
| − | In jedem Drachenviereck sind zwei benachbarte Seiten kongruent (gleichlang) zueinander. Paul definiert: Wenn in einem Viereck zwei benachbarte Seiten kongruent zueinander sind, ist das Viereck ein Drachen. | + | In jedem Drachenviereck sind zwei benachbarte Seiten kongruent (gleichlang) zueinander. Paul definiert: Wenn in einem Viereck zwei benachbarte Seiten kongruent zueinander sind, ist das Viereck ein Drachen. Wie man leicht sieht umfasst diese Definition jedoch auch Vierecke, die wir nicht als Drachen ansehen wollen.<br /> |
| − | <ggb_applet width="529" height="404" version="4.2" ggbBase64="UEsDBBQACAgIAPyElUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAPyElUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vptb9s4Ev7c/RWEsB9jme+SCqcLJ93FFWj3ik33cLgvC1qibW5kSSfJjl30x9+QlPwSN0mdZA/p4dI4FMnhDOftmVGa0U/rRY5Wum5MWZwHJMQB0kVaZqaYnQfLdjqIg5/e/DCa6XKmJ7VC07JeqPY84CENdudgFjJ32GTnAY4p0SmOBqmaxgPOYj6IccYHXCRTRhWZcjYNEFo35nVR/qoWuqlUqq/SuV6o92WqWsdz3rbV6+Hw5uYm7KWHZT0bzmaTcN1kAYKbF8150D28BnYHh26YI6cYk+E/P7z37AemaFpVpDpAVqulefPDq9GNKbLyBt2YrJ2fB0LIAM21mc1BTcFJgIaWqAJdK522ZqUbOLo3dTq3iypwZKqw+6/8E8q36gQoMyuT6RrsEzKRRIRShikRMY1YgMra6KLtaHuZw57baGX0jWdrn5xEjpMIXGAaM8n1eTBVeQNamWJag0XhQvUSpk27yfVE1f18dx9yBv+AwHzWlhe4zpvhPKAJPqMkOoswPhMC+7vsCw5QW5a544qRSNCXL4hiitGZHYgfKAxS+i3s1zDzA/UD94PwNNwf556UexruaTi7R89uvlO0WzjQtNeT7etJQD/7kfBxBrilZ7ynJ7FKfEHE3t4NDNl7E3d/O/BuKv00cgPBfiDdZmx/OHvJJ2rEHqUR2ZPq4+FuoUfx0ksUNPl2ifRJem61pF/Tkoo7tHyicXuhROwJBVnu232ORLKT9LzTtCdIlPwpuf8IgRH+bwgcDXukG3W5h5q5pe3CtdWLxqIOSxzwIIIEJKaMACcEIgkMkU1QiohAXMCUxEjaMULM5iRHDMXI0hGGHLyIGH5wl68SCeBlFyOfuIhxJBgiDpQ4AihCDtgA5CgDCiGQgENWOrFimURcwoTFiMMFLaRFFjYYnIM5CKeIEcTsWRIhKpGkKLKwSLhFSxnbuwNTiiRG0h4FXARM9HgIJ2LErDYQ4VXZmK1x5zqvtl5xdjRFtWwPbJcusv6xLW9RZ2V6fXHL1lo1bf8MRFCMdiXPF6eDivhqlKuJzqFvuLJhgNBK5TaDHf9pWbSoDwHq12a1quYmba5028KpBv2pVuq9avX6F6Bu+gs60a5Qj/QyzU1mVPEPiBHLwjJE27ptcamv2yySXkpalnV2tWkgcND6X7ou4QKE2U5l081EEuL9Lws6qbJRLvDhDhh6023xJEz2v2IvTa+22qi13uqAZrVNob3Ju+aizHdLVWmK9lJV7bJ2jRfcobaKjItZrp09HZRCC5NeT8r1lTck87w+bSqYYX+DyeyyzMsaQRJSIYCgGyd+dDT2alsq7Giwo8C9Z0y23ScJdRRunPjRUYGr/dU6VUmvJsG9GNP4fjDoAqvHWhsotiNaFqZ9309ak153qhJ/4NflYgIx1gXhIU/yXDxHw1thNbrWdaFzHzwFOHNZLhsfzduIfDVaNvqjaufjIvtNzyANPyqLhC2w9qS7K2c6NQs46Nc74ynr2N/hqn4107Na9yrmrtf1pnW7eD+Uj5Ydq1/qcvGuWH2CqLl11dGw12fUpLWpbHSiCUDztd7FX2YaBcCe7Z8D5RvQIrUgA4ZsrREDpJbtvKxdOwupCvoQNK5qkwM2QjzaJM31AjpZ1LqodIG99c4H1yJbN6By8idAx7ZS+P2d0WD7jghFKq/myjbRnf652uj6wCKO24cy0wcYpApwg1MGwKDyAVFp7WPJ3xYeKmDnUnDP187wDVqfBwMScii8GyuewMNn/8rkXxCsqjYzD6T61WNfQq7bq7i1H8c/dpHobeeMv1ioIkOFK6+Xpk5zHexwXWFrTKSI7ca9wZZtv5F6Zh2LI5eAX026NXl67JLDjNqzw3M6Bd8GkRZqwTW87TQO6doO09zD30yWaVfoPMiamS5WcNUSkg2tcffausFePvrcr6zBPAO3tCHd0mey5zEIh9qs0binH/dUY2pdzcIES3gJGLOO8ZjbfRsAY+E4k874+t+FV6LxWGPLopma9H6vfnS5cejU9Mib4/u9eZhg44e8+fUMI9RXCjd2leLRLn2WPMMhl0ksIg6lVXApY591AxZGHIvIVmMRE0ajxyfhUx1zcYpjLv5HHENCFsXcuiShjDP7Zg5uoWESxYyxRMRccIYp+wu84kFwXKdfx8ExDLTzyoGfsm+Aw0rVO19lD1Sp/yPi6YhoFlVuUtNuvZPbIHtX2IZJuxbjuMW61rqyve3fi0+1Khr7m8fD3uq0DM6OIuPylAy+fEm9Cxj6EcmLw5hikcQ0iXnEGJVJD6rwEpQIFrMYXnJg99kam4sHGptv89PbU/z09vv3Ew0B50kEzuIykjGjHmVJKCMiBCcUIBYqIhPP5qe3R366z8Q/f/8mjkImffCTkD5fvF8+GO/5ZlYWX69gl76C/QwD64L+IA3g9TSH93/iqReeOv2DeHowvwI0zv4gD2WLv0LvrC3XxxafkwslEcyFgiBHsUBOqZV3h2ujZ3a2vcjicRX9noueWNR3gcdCmtzCWtdAUbmPzJGLSB5CjnOeRJInTEjMHt8h/AUV936T27h8MUaHJI+jY6vLULCEYxJhIqiUke9aKTgD4DXhnArJmUzkd2R2/YKMDm8F4qBeRR5xRUgwjymJwCGUERl3dQzW4wT8wIWMIQ3I9xTu2UsKdwJxfWB41vd5MjnoK6gP+DCiNJI0jiMppCTkRdl9uP97SPd/Ad0fA7z5D1BLBwjbn8QA9gcAALwgAABQSwECFAAUAAgICAD8hJVC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAPyElULbn8QA9gcAALwgAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAjQgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | + | <ggb_applet width="529" height="404" version="4.2" ggbBase64="UEsDBBQACAgIAPyElUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAPyElUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vptb9s4Ev7c/RWEsB9jme+SCqcLJ93FFWj3ik33cLgvC1qibW5kSSfJjl30x9+QlPwSN0mdZA/p4dI4FMnhDOftmVGa0U/rRY5Wum5MWZwHJMQB0kVaZqaYnQfLdjqIg5/e/DCa6XKmJ7VC07JeqPY84CENdudgFjJ32GTnAY4p0SmOBqmaxgPOYj6IccYHXCRTRhWZcjYNEFo35nVR/qoWuqlUqq/SuV6o92WqWsdz3rbV6+Hw5uYm7KWHZT0bzmaTcN1kAYKbF8150D28BnYHh26YI6cYk+E/P7z37AemaFpVpDpAVqulefPDq9GNKbLyBt2YrJ2fB0LIAM21mc1BTcFJgIaWqAJdK522ZqUbOLo3dTq3iypwZKqw+6/8E8q36gQoMyuT6RrsEzKRRIRShikRMY1YgMra6KLtaHuZw57baGX0jWdrn5xEjpMIXGAaM8n1eTBVeQNamWJag0XhQvUSpk27yfVE1f18dx9yBv+AwHzWlhe4zpvhPKAJPqMkOoswPhMC+7vsCw5QW5a544qRSNCXL4hiitGZHYgfKAxS+i3s1zDzA/UD94PwNNwf556UexruaTi7R89uvlO0WzjQtNeT7etJQD/7kfBxBrilZ7ynJ7FKfEHE3t4NDNl7E3d/O/BuKv00cgPBfiDdZmx/OHvJJ2rEHqUR2ZPq4+FuoUfx0ksUNPl2ifRJem61pF/Tkoo7tHyicXuhROwJBVnu232ORLKT9LzTtCdIlPwpuf8IgRH+bwgcDXukG3W5h5q5pe3CtdWLxqIOSxzwIIIEJKaMACcEIgkMkU1QiohAXMCUxEjaMULM5iRHDMXI0hGGHLyIGH5wl68SCeBlFyOfuIhxJBgiDpQ4AihCDtgA5CgDCiGQgENWOrFimURcwoTFiMMFLaRFFjYYnIM5CKeIEcTsWRIhKpGkKLKwSLhFSxnbuwNTiiRG0h4FXARM9HgIJ2LErDYQ4VXZmK1x5zqvtl5xdjRFtWwPbJcusv6xLW9RZ2V6fXHL1lo1bf8MRFCMdiXPF6eDivhqlKuJzqFvuLJhgNBK5TaDHf9pWbSoDwHq12a1quYmba5028KpBv2pVuq9avX6F6Bu+gs60a5Qj/QyzU1mVPEPiBHLwjJE27ptcamv2yySXkpalnV2tWkgcND6X7ou4QKE2U5l081EEuL9Lws6qbJRLvDhDhh6023xJEz2v2IvTa+22qi13uqAZrVNob3Ju+aizHdLVWmK9lJV7bJ2jRfcobaKjItZrp09HZRCC5NeT8r1lTck87w+bSqYYX+DyeyyzMsaQRJSIYCgGyd+dDT2alsq7Giwo8C9Z0y23ScJdRRunPjRUYGr/dU6VUmvJsG9GNP4fjDoAqvHWhsotiNaFqZ9309ak153qhJ/4NflYgIx1gXhIU/yXDxHw1thNbrWdaFzHzwFOHNZLhsfzduIfDVaNvqjaufjIvtNzyANPyqLhC2w9qS7K2c6NQs46Nc74ynr2N/hqn4107Na9yrmrtf1pnW7eD+Uj5Ydq1/qcvGuWH2CqLl11dGw12fUpLWpbHSiCUDztd7FX2YaBcCe7Z8D5RvQIrUgA4ZsrREDpJbtvKxdOwupCvoQNK5qkwM2QjzaJM31AjpZ1LqodIG99c4H1yJbN6By8idAx7ZS+P2d0WD7jghFKq/myjbRnf652uj6wCKO24cy0wcYpApwg1MGwKDyAVFp7WPJ3xYeKmDnUnDP187wDVqfBwMScii8GyuewMNn/8rkXxCsqjYzD6T61WNfQq7bq7i1H8c/dpHobeeMv1ioIkOFK6+Xpk5zHexwXWFrTKSI7ca9wZZtv5F6Zh2LI5eAX026NXl67JLDjNqzw3M6Bd8GkRZqwTW87TQO6doO09zD30yWaVfoPMiamS5WcNUSkg2tcffausFePvrcr6zBPAO3tCHd0mey5zEIh9qs0binH/dUY2pdzcIES3gJGLOO8ZjbfRsAY+E4k874+t+FV6LxWGPLopma9H6vfnS5cejU9Mib4/u9eZhg44e8+fUMI9RXCjd2leLRLn2WPMMhl0ksIg6lVXApY591AxZGHIvIVmMRE0ajxyfhUx1zcYpjLv5HHENCFsXcuiShjDP7Zg5uoWESxYyxRMRccIYp+wu84kFwXKdfx8ExDLTzyoGfsm+Aw0rVO19lD1Sp/yPi6YhoFlVuUtNuvZPbIHtX2IZJuxbjuMW61rqyve3fi0+1Khr7m8fD3uq0DM6OIuPylAy+fEm9Cxj6EcmLw5hikcQ0iXnEGJVJD6rwEpQIFrMYXnJg99kam4sHGptv89PbU/z09vv3Ew0B50kEzuIykjGjHmVJKCMiBCcUIBYqIhPP5qe3R366z8Q/f/8mjkImffCTkD5fvF8+GO/5ZlYWX69gl76C/QwD64L+IA3g9TSH93/iqReeOv2DeHowvwI0zv4gD2WLv0LvrC3XxxafkwslEcyFgiBHsUBOqZV3h2ujZ3a2vcjicRX9noueWNR3gcdCmtzCWtdAUbmPzJGLSB5CjnOeRJInTEjMHt8h/AUV936T27h8MUaHJI+jY6vLULCEYxJhIqiUke9aKTgD4DXhnArJmUzkd2R2/YKMDm8F4qBeRR5xRUgwjymJwCGUERl3dQzW4wT8wIWMIQ3I9xTu2UsKdwJxfWB41vd5MjnoK6gP+DCiNJI0jiMppCTkRdl9uP97SPd/Ad0fA7z5D1BLBwjbn8QA9gcAALwgAABQSwECFAAUAAgICAD8hJVC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAPyElULbn8QA9gcAALwgAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAjQgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> |
| + | ====Beispiel 2==== | ||
| + | Lisa will den Begriff des Rechtecks über die Eigenschaften der Diagonalen aller Rechtecke definieren:<br /> | ||
| + | Ein Viereck dess Diagonalen kongruent zueinander sind, sich jeweils halbieren und senkrecht aufeinander stehen heißt Rechteck.<br /> | ||
| + | Alle Vierecke, die Lisas Definition entsprechen sind auf jeden Fall Rechtecke. Sie sind sogar Quadrate, allerdings auch nur Quadrate. Lisas Definition umfasst kein Rechteck, das kein Quadrat ist. | ||
==Minimalität mathematischer Definitionen== | ==Minimalität mathematischer Definitionen== | ||
| − | === | + | ===Beispiele=== |
| + | ====Beispiel 1==== | ||
| + | Parallelogramme haben folgende Eigenschaften: | ||
| + | #Die gegeüberliegenden Seiten sind parallel zueinander. | ||
| + | #Die gegenüberliegenden seiten sind kongruent zueinander. | ||
| + | #Gegenüberliegende Innenwinkel sind kongruent zueinander. | ||
| + | #Die Diagonalen halbieren jeweils einander. | ||
| + | #Benachbarte Innenwinkel sind supplementär (ergänzen sich zu 180°). | ||
| + | Man könnte jetzt meinen, dass es sinnvoll wäre alle dies Eigenschaften zur definition des Begriffs ''Parallelogramm'' zu verwenden. Das würde die Definition aber nur unnötig aufblähen. Aus diesem Grund wählt man die definierende Eigenschaft des zu definierenden Begriffs derart, dass sie gerade so ausreichend ist, den Begriff exakt zu definieren. Alle die Eigenschaften unseres definierten Begriffs, die aus der Definition beweisbar wären, werden in sogenannten Sätzen verwigt, jedoch nicht in der Definition aufgeführt. | ||
| + | <br /> | ||
| + | {{Definition|1=Jedes Viereck dessen gegenüberliegende Seiten parallel zueinander sind, heißt Parallelogramm.}} | ||
| + | Natürlich hat jedes Viereck, das nach dieser Definition als Parallelogramm zu identifizieren ist die Eigenschaft, dass seine gegenüberliegenden Seiten kongruent zueinander sind. | ||
| + | Diese Eigenschaft schreibe wir in einem Satz auf:<br /> | ||
| + | '''Satz über die gegeüberliegenden Seiten im Parallelogramm:'''<br /> | ||
| + | :Wenn ein Viereck ein Parallelogramm ist, so sind seine gegenüberliegenden Seiten kongruent zueinander. | ||
| + | <br /> | ||
| + | Sätze müssen bewiesen werden:<br /> | ||
| + | '''Beweis des Satzes über die gegenüberliegenden Seiten des Parallelogramms:'''<br /> | ||
| + | Es sei <math>\overline{ABCD}</math> ein Parallelogramm. Entsprechend der Definition des Begriss Parallelogramm gilt: | ||
| + | <br /> | ||
| + | Voraussetzung 1: <math>AB || CD</math><br /> | ||
| + | Voraussetzung 2: <math>AD || BC </math><br /> | ||
| + | (I) Wegen Voraussetzung 1 und dem Wechselwinkelsatz gilt: <math>\angle CAB \tilde= \angle ACD</math><br /> | ||
| + | (II) Wegen Voraussetzung 2 und dem Wechselwinkelsatz gilt: <math>\angle ACB \tilde= \angle CAD</math><br /> | ||
| + | (III) Trivialerweise ist die Diagonale <math>\overline{AC}</math> zu sich selbst kongruent.<br /> | ||
| + | (IV) Wegen (I), (II), (III) und WSW gilt: <math>\overline{ABC} \tilde= \overline{CBA}</math><br /> | ||
| + | (V) Nach Definition sind Dreiecke dann und nur dann kongruent, wenn sie in allen Bestimmungstücken (Seiten und Winkel) übereinstimmen. Entsprechend (IV) müssem demnach die gegenüberliegenden Seiten von <math>\overline{ABCD}</math> kongruent zueinander sein. | ||
=Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulieren= | =Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulieren= | ||
Aktuelle Version vom 21. April 2013, 16:22 Uhr
|
Aufgaben vorabDefinieren Sie:
Was ist eine Definition?Rein aus der Intuition herausZuordnung
Was ist nun eine DefinitionEs ist schwer den Begriff mathematische Definition sauber zu klären (zu definieren). Wir wollen unter einer Definition die Beschreibung, Festlegung eines Begriffes verstehen. Aus mathematischer Sicht sind an eine derartige Begriffsbeschreibung gewisse Forderungen zu stellen. Was sind mathematische Definitionen?Ein QuizFazitWill man eine Begriffsbeschreibung effizient erstellen, so wird man sinnvollerweise auf andere Begriffe zurückgreifen. All diese Begriffe müssen ihrerseits vorab festgelegt worden sein. undefinierte Grundbegriffe
Irgendwann sind wir mit der Rückführung auf andere Begriffe am Ende. Wir müssen akzeptieren, dass wir nicht alles sauber und exakt definieren können, obwohl wir doch sehr genaue Vorstellungen von unserem Begriff haben. Der Mathematiker geht dann von sogenannten undefinierten Grundbegriffen aus:
Wir ergänzen:Eine mathematische Definition ist eine Begriffsbeschreibung, die nur bereits definierte Begriffe bzw. als undefiniert festgelegte Grundbegriffe verwendet. Exaktheit und Minimalität mathematischer DefinitionenEine Definition muss den Begriff und nur den Begriff exakt beschreibenEin QuizBeispieleBeispiel 1In jedem Drachenviereck sind zwei benachbarte Seiten kongruent (gleichlang) zueinander. Paul definiert: Wenn in einem Viereck zwei benachbarte Seiten kongruent zueinander sind, ist das Viereck ein Drachen. Wie man leicht sieht umfasst diese Definition jedoch auch Vierecke, die wir nicht als Drachen ansehen wollen. Beispiel 2Lisa will den Begriff des Rechtecks über die Eigenschaften der Diagonalen aller Rechtecke definieren: Minimalität mathematischer DefinitionenBeispieleBeispiel 1Parallelogramme haben folgende Eigenschaften:
Man könnte jetzt meinen, dass es sinnvoll wäre alle dies Eigenschaften zur definition des Begriffs Parallelogramm zu verwenden. Das würde die Definition aber nur unnötig aufblähen. Aus diesem Grund wählt man die definierende Eigenschaft des zu definierenden Begriffs derart, dass sie gerade so ausreichend ist, den Begriff exakt zu definieren. Alle die Eigenschaften unseres definierten Begriffs, die aus der Definition beweisbar wären, werden in sogenannten Sätzen verwigt, jedoch nicht in der Definition aufgeführt.
Definition Jedes Viereck dessen gegenüberliegende Seiten parallel zueinander sind, heißt Parallelogramm. Natürlich hat jedes Viereck, das nach dieser Definition als Parallelogramm zu identifizieren ist die Eigenschaft, dass seine gegenüberliegenden Seiten kongruent zueinander sind.
Diese Eigenschaft schreibe wir in einem Satz auf:
Genau dasselbe, nur ganz anders: Arten, Definitionen zu formulierenEs gibt verschiedene Arten, Definitionen zu formulieren. Beispiel 1: ggT zweier ganzer ZahlenDie Begriffe Teiler und Euklidischer Algorithmus seien im Folgenden bereits exakt definiert. Das Übliche, die Realdefinition
Konventionaldefinition, das Ganze in "wenn-dann"
Schön, aber wie bekomme ich den ggT: die genetisch, operative Definition
Beispiel 2: DrachenviereckDie Begriffe Dreieck, Viereck, Diagonale, Eckpunkt, Geradenspiegelung und achsensymmetrisch seien im Folgenden bereits definiert. Realdefinition
Konventionaldefinition
genetisch, operative Definition
Ein wenig Didaktik: Definitionen auf verschiedenen NiveaustufenAus didaktischer Sicht lassen sich Definitionen auf verschiedenen Niveaustufen formulieren.
Entwicklung einer "neuen" DefinitionGärtnerkonstruktion der EllipseVideoIm Folgenden wollen wir versuchen, den (ihnen vermutlich wenig geläufigen) Begriff Ellipse zu definieren. Konstruktiv lässt sich eine Ellipse mit Hilfe der sogenannten Gärtnerkonstruktion, wie im folgenden Video, erzeugen. EmbedVideo erhielt die unbrauchbare ID „PQjeTmY0cdQ&NR=1“ für „youtube“.
Bemerkung zu obigem Video: Das geht natürlich noch schöner. Ansporn für Sie? AppletDas folgende Applet empfindet die Gärtnerkonstruktion nach. Aufgaben zur Gärtnerkonstruktion
Vereinbarung: Wir setzen ebene Geometrie voraus. Definition E.1: EllipseAlle Punkte P (mit P liegt in der Ebene E und alle P Element k) für die gilt: Strecke AP + Strecke BP = q (q sei eine feste Zahl).--Natürliches Mineralwasser 15:02, 17. Jan. 2013 (CET) Definition K.1: Kreis als spezielle Ellipse... Zurückführen auf bereits vorhanden Definitionen: Verwenden von OberbegriffenDas Haus der Vierecke
[ www.ph-heidelberg.de is not an authorized iframe site ]
|
 mit Mittelpunkt
mit Mittelpunkt  und Radius
und Radius 
 ist die Menge aller Punkte, die zwischen den Punkten
ist die Menge aller Punkte, die zwischen den Punkten  und
und  liegt vereinigt mit der Menge, die aus den Punkten
liegt vereinigt mit der Menge, die aus den Punkten  ein Parallelogramm. Entsprechend der Definition des Begriss Parallelogramm gilt:
ein Parallelogramm. Entsprechend der Definition des Begriss Parallelogramm gilt:
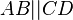
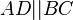
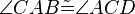
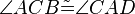
 zu sich selbst kongruent.
zu sich selbst kongruent.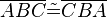
 und
und  zwei ganze Zahlen.
zwei ganze Zahlen. 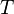 sei die Menge aller Zahlen, die sowohl Teiler von
sei die Menge aller Zahlen, die sowohl Teiler von  sowohl die ganze Zahl
sowohl die ganze Zahl  gibt, die auch
gibt, die auch  ein Dreieck und
ein Dreieck und 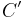 das Bild von
das Bild von  bei der Spiegelung an
bei der Spiegelung an  . Das Viereck
. Das Viereck 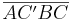 ist ein Drachenviereck.
ist ein Drachenviereck.

