Übungen 03: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Aufgabe 2) |
(→Aufgabe 1) |
||
| Zeile 1: | Zeile 1: | ||
=Aufgabe 1= | =Aufgabe 1= | ||
| − | Gegeben sind | + | Gegeben sind drei Ebenengleichungen <math>a_1x+b_1y+c_1z=d_1</math>, <math>a_2x+b_2y+c_2z=d_2</math> und <math>a_3x+b_3y+c_3z=d_3</math>.<br />.<br /> |
| − | Geben Sie | + | Geben Sie drei Ebenen dieser Form an, sodass das LGS dazu |
a) genau eine Lösung <br /> | a) genau eine Lösung <br /> | ||
| Zeile 10: | Zeile 10: | ||
hat.<br /> | hat.<br /> | ||
Was bedeutet das anschaulich für die Lage der Ebenen? | Was bedeutet das anschaulich für die Lage der Ebenen? | ||
| − | |||
=Aufgabe 2= | =Aufgabe 2= | ||
Bestimmen Sie ein lineares Gleichungssystem (bestehend aus zwei Gleichungen), das die Gerade durch die Punkte <math>P(0|5|-2)</math> und <math>Q(14|3|2)</math> beschreibt. Tipp: Überlegen Sie sich, was das geometrisch repräsentiert. | Bestimmen Sie ein lineares Gleichungssystem (bestehend aus zwei Gleichungen), das die Gerade durch die Punkte <math>P(0|5|-2)</math> und <math>Q(14|3|2)</math> beschreibt. Tipp: Überlegen Sie sich, was das geometrisch repräsentiert. | ||
Version vom 29. April 2013, 14:54 Uhr
Aufgabe 1
Gegeben sind drei Ebenengleichungen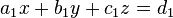 
, 
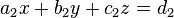und 
.
.
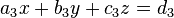Geben Sie drei Ebenen dieser Form an, sodass das LGS dazu
a) genau eine Lösung
b) keine Lösung
c) eine ein-parametrige Lösung
d) eine zwei-parametrige Lösung
hat.
Was bedeutet das anschaulich für die Lage der Ebenen?
Aufgabe 2
Bestimmen Sie ein lineares Gleichungssystem (bestehend aus zwei Gleichungen), das die Gerade durch die Punkte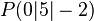 
und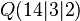 
beschreibt. Tipp: Überlegen Sie sich, was das geometrisch repräsentiert.
