Beweisen SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Behauptung) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 2: Innenwinkelsatz für Dreiecke) |
||
| Zeile 33: | Zeile 33: | ||
====Beispiel 2: Innenwinkelsatz für Dreiecke==== | ====Beispiel 2: Innenwinkelsatz für Dreiecke==== | ||
=====Ohne Wenn-Dann===== | =====Ohne Wenn-Dann===== | ||
| − | ::In jedem Dreieck beträgt die Summe der Größen seiner Innenwinkel <math> | + | ::In jedem Dreieck beträgt die Summe der Größen seiner Innenwinkel <math>180</math>°. |
=====Wenn-Dann-Form===== | =====Wenn-Dann-Form===== | ||
| − | Wenn ein n-Eck ein Dreieck ist, dann beträgt die Summe der Größen seiner Innenwinkel <math> | + | ::Wenn ein n-Eck ein Dreieck ist, dann beträgt die Summe der Größen seiner Innenwinkel <math>180</math>°. |
=====Voraussetzung===== | =====Voraussetzung===== | ||
: Das betrachtetet n-Eck ist ein Dreieck | : Das betrachtetet n-Eck ist ein Dreieck | ||
=====Behauptung===== | =====Behauptung===== | ||
: Die Summe der Größen seiner Innenwinkel beträgt <math>180</math>°. | : Die Summe der Größen seiner Innenwinkel beträgt <math>180</math>°. | ||
| + | ====Beispiel 3==== | ||
| + | =====Ohne Wenn-Dann===== | ||
| + | ::Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der längsten Seite dieses Dreiecks. | ||
| + | =====Wenn-Dann-Form===== | ||
| + | :: Wenn ein Dreieck rechtwinklig ist, dann liegt der Mittelpunkt seines Umkreises auf der längsten seiner Seiten. | ||
| + | =====Voraussetzung===== | ||
| + | : Das betrachtete Dreieck ist rechtwinklig | ||
| + | =====Behauptung===== | ||
| + | : Der Mittelpunkt seines Umkreises liegt auf der längsten seiner Seiten. | ||
<!--- ------------------------------------------------------------- ---> | <!--- ------------------------------------------------------------- ---> | ||
Version vom 2. Mai 2013, 18:15 Uhr
ImplikationenBeispieleBeispiel 1Wenn der BVB im Finale der Champions League das erste Tor des Spieles schießt, dann gewinnt er die Champions League der Saison 2012/13. Beispiel 2Wenn ein Trapez ein Rechteck ist, dann sind sein Diagonalen kongruent zueinander. Beispiel 3Wenn ein Boxer während des Kampfes seinem Gegner den Rücken zukehrt, hat er den Kampf verloren. Beispiel 4Wenn zwei Winkel Stufenwinkel an geschnittenen Parallelen sind, dann sind sie kongruent zueinander. Grundlegender Aufbau
Zusammenhang zur hinreichenden BedingungIst die Aussage "Versteckte" ImplikationenBeispieleBeispiel 1: StufenwinkelsatzOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Beispiel 2: Innenwinkelsatz für DreieckeOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Beispiel 3Ohne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
|
 , dann Behauptung
, dann Behauptung  .
.

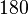 °.
°.

