Serie 3 SoSe 2013: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.01 SoSe 2013 S) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.02 SoSe 2013 S) |
||
| Zeile 11: | Zeile 11: | ||
# ''stumpfer Winkel'' | # ''stumpfer Winkel'' | ||
| − | =Aufgabe 3.02 SoSe 2013 S= | + | ==Aufgabe 3.02 SoSe 2013 S== |
Die Begriffe Dreieck, Seiten eines Dreiecks, Eckpunkte eines Dreiecks und Innenwinkel eines Dreiecks seien bereits exakt definiert worden. | Die Begriffe Dreieck, Seiten eines Dreiecks, Eckpunkte eines Dreiecks und Innenwinkel eines Dreiecks seien bereits exakt definiert worden. | ||
Definieren Sie mathematisch korrekt die Begriffe: | Definieren Sie mathematisch korrekt die Begriffe: | ||
Version vom 4. Mai 2013, 17:42 Uhr
Definitionen und DefinierenAufgabe 3.01 SoSe 2013 SDie Begriffe Winkel, Schenkel eines Winkels, Scheitel eines Winkels und Größe eines Winkels seien bereits mathematisch exakt definiert. Definieren Sie Form einer mathematisch korrekten Konventionaldefinitionen die Begriffe:
Aufgabe 3.02 SoSe 2013 SDie Begriffe Dreieck, Seiten eines Dreiecks, Eckpunkte eines Dreiecks und Innenwinkel eines Dreiecks seien bereits exakt definiert worden. Definieren Sie mathematisch korrekt die Begriffe:
Aufgabe 3.03 SoSe 2013 SWarum handelt es sich im Folgenden nicht um eine korrekte Definition?
Aufgabe 3.04 SoSe 2013 SFür die Schule hat man sich auf eine besondere Art der Bezeichnung der Stücke von Dreiecken geeinigt.
Definieren Sie den Begriff allgemeine schulübliche Dreieckbezeichnungen. Aufgabe 3.05 SoSe 2013Definieren Sie die Begriffe:
Implikationen, Begründen und BeweisenAufgabe 3.06 SoSe 2013 |
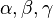 bezeichnet.
bezeichnet.
 bezeichnet.
bezeichnet.
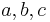 bezeichnet.
bezeichnet.

