Serie 3 SoSe 2013: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.07 SoSe 2013) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.07 SoSe 2013) |
||
| Zeile 46: | Zeile 46: | ||
Beweisen Sie: Der prozentuale Anteil der schraffierten Flächen in Bezug auf die Fläche des jeweiligen Quadrats <math>\overline{ABCD}</math> bzw.<math>\overline{EFGH}</math> ist gleich. | Beweisen Sie: Der prozentuale Anteil der schraffierten Flächen in Bezug auf die Fläche des jeweiligen Quadrats <math>\overline{ABCD}</math> bzw.<math>\overline{EFGH}</math> ist gleich. | ||
| − | ==Aufgabe 3.07 SoSe 2013== | + | ==Aufgabe 3.07 SoSe 2013 S== |
Gegeben sei ein Dreieck <math>\overline{ABC}</math> mit dem Umkreis <math>k</math>. Der Mittelpunkt von <math>k</math> möge ein Punkt der Strecke <math>\overline{AB}</math> sein. Der Winkel <math>\angle CAB</math> habe die Größe <math>25</math>°. Berechnen Sie die folgenden Winkelgrößen: | Gegeben sei ein Dreieck <math>\overline{ABC}</math> mit dem Umkreis <math>k</math>. Der Mittelpunkt von <math>k</math> möge ein Punkt der Strecke <math>\overline{AB}</math> sein. Der Winkel <math>\angle CAB</math> habe die Größe <math>25</math>°. Berechnen Sie die folgenden Winkelgrößen: | ||
# <math>|\angle ACM|</math> | # <math>|\angle ACM|</math> | ||
| Zeile 60: | Zeile 60: | ||
* Basiswinkelsatz für gleichschenklige Dreiecke | * Basiswinkelsatz für gleichschenklige Dreiecke | ||
| + | ==Aufgabe 3.08 SoSe 2013 S== | ||
| + | Formulieren Sie den Satz des Pythagoras in der Form Wenn-Dann. Nennen Sie dann noch einmal explizit die Voraussetzung und die Behauptung des Satzes. | ||
| + | |||
| + | ==Aufgabe 3.09 SoSe 2013 S== | ||
| + | Unter der Umkehrung einer Implikation <math>a \Rightarrow b</math> versteht man die Implikation <math>b \Rightarrow a</math> (Voraussetzung und Behauptung werden getauscht). | ||
| + | |||
| + | # Formulieren Sie die Umkehrung des Satzes von Pythagoras | ||
| + | # Entscheiden Sie (ohne Beweis), ob die Umkehrung des Satzes von Pythagoras eine wahre Aussage ist. | ||
| + | # Oberstudienrätin Schultze-Kröttendörfer läßt ihre 9a die Seiten von Dreiecken vermessen, Quadrate der gemessenen Dreieckseiten bilden, diese Quadrate in geeigneter Weise addieren und vergleichen. Aus diesen Vergleichen sollen die Schüler explizit entscheiden, ob die untersuchten Dreiecke rechtwinklig sind oder nicht. Wenden die Schüler zu dieser Entscheidung den Satz des Pythagoras oder seine Umkehrung an? Begründen Sie Ihre Entscheidung. | ||
| + | |||
| + | ==Aufgabe 3.10 SoSe 2013 S= | ||
| + | Der Satz des Pythagoras sei bewiesen. Formulieren Sie nun den Höhensatz des Euklid und beweisen Sie ihn nur unter Verwednung des Satzes von Pythagoras. | ||
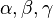 bezeichnet.
bezeichnet.
 bezeichnet.
bezeichnet.
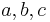 bezeichnet.
bezeichnet.
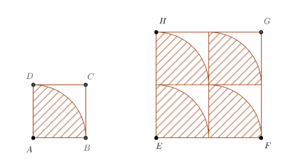
 und
und 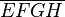 seien Quadrate. Die einzelnen schraffierten Punktmengen seien das Innere von Viertelkreisen.
seien Quadrate. Die einzelnen schraffierten Punktmengen seien das Innere von Viertelkreisen. mit dem Umkreis
mit dem Umkreis  . Der Mittelpunkt von
. Der Mittelpunkt von  sein. Der Winkel
sein. Der Winkel 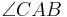 habe die Größe
habe die Größe 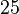 °. Berechnen Sie die folgenden Winkelgrößen:
°. Berechnen Sie die folgenden Winkelgrößen:
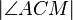
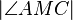
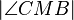
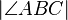
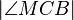
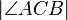
 versteht man die Implikation
versteht man die Implikation 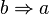 (Voraussetzung und Behauptung werden getauscht).
(Voraussetzung und Behauptung werden getauscht).

