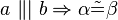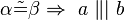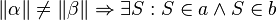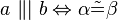Lösung von Aufgabe 3.3 (SoSe 13 P): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 16: Zeile 16:
 
*Selbe Problematik wie in (1) und (2).--[[Benutzer:Nolessonlearned|Nolessonlearned]] 17:13, 7. Mai 2013 (CEST)<br />
 
*Selbe Problematik wie in (1) und (2).--[[Benutzer:Nolessonlearned|Nolessonlearned]] 17:13, 7. Mai 2013 (CEST)<br />
  
−
Der Text am Anfang von b ist Voraussetzung für die einzelnen Implikationen und gehört jeweils dazu. Somit brauch c nicht in der Implikation vorkommen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:17, 8. Mai 2013 (CEST)
+
Der Text am Anfang von b) ist Voraussetzung für die einzelnen Implikationen und gehört jeweils dazu. Somit brauch c nicht in der Implikation vorkommen.<br />
 
- Welche Aussagen sind äquivalent zum Stufenwinkelsatz?<br />
 
- Welche Aussagen sind äquivalent zum Stufenwinkelsatz?<br />
−
- Könnt ihr die Aussagen genauer benennen im Verhältnis zur Implikation des Stufenwinkelsatzes?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:17, 8. Mai 2013 (CEST)
+
- Könnt ihr die Aussagen genauer benennen?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:17, 8. Mai 2013 (CEST)
  
 
[[Category:Einführung_P]]
 
[[Category:Einführung_P]]

Version vom 8. Mai 2013, 18:18 Uhr

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel \alpha und \beta . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?

  1. \ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta
  • Es fehlt der Bezug zur Gerade c.--Nolessonlearned 17:13, 7. Mai 2013 (CEST)


  1. \alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b
  • Umkehrung von (1). Gleiche Problematik wie in (1).--Nolessonlearned 17:13, 7. Mai 2013 (CEST)


  1. \|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b
  • Äquivalente Aussage zum Stufenwinkelsatz. Logischer Zusammenhang.--Nolessonlearned 16:59, 7. Mai 2013 (CEST)


  1. \ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta
  • Selbe Problematik wie in (1) und (2).--Nolessonlearned 17:13, 7. Mai 2013 (CEST)

Der Text am Anfang von b) ist Voraussetzung für die einzelnen Implikationen und gehört jeweils dazu. Somit brauch c nicht in der Implikation vorkommen.
- Welche Aussagen sind äquivalent zum Stufenwinkelsatz?
- Könnt ihr die Aussagen genauer benennen?--Tutorin Anne 19:17, 8. Mai 2013 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_3.3_(SoSe_13_P)&oldid=23038“