Beweisen SoSe 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Bespiel 2: Eindeutigkeit des Lotes von einem Punkt auf eine Gerade) |
*m.g.* (Diskussion | Beiträge) (→Die Beweisführung) |
||
| Zeile 153: | Zeile 153: | ||
::Es gibt zwei zueinander verschiedene Lote <math>l_1</math> und <math>l_2</math> von <math>P</math> auf <math>g</math>. | ::Es gibt zwei zueinander verschiedene Lote <math>l_1</math> und <math>l_2</math> von <math>P</math> auf <math>g</math>. | ||
====Die Beweisführung==== | ====Die Beweisführung==== | ||
| − | [[Datei:Eindeutigkeit des Lotes.png|200px]] | + | [[Datei:Eindeutigkeit des Lotes.png|200px]]<br /> |
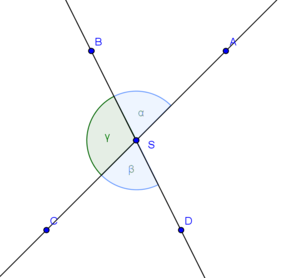
| + | # Es sei <math>\alpha</math> der Nebenwinkel zu <math>\angle PL_1L_2</math> | ||
| + | # Weil <math>l_1</math> Lot von <math>P</math> auf <math>g</math> ist, hat <math>\alpha</math> die Größe <math>90^\circ</math>. | ||
| + | # Der Winkel <math>\beta=\angle PL_2L_1</math> hat ebenso die Größe <math>90^\circ</math>, denn auch <math>l_2</math> ist Lot von <math>P</math> auf <math>g</math>. | ||
| + | # Nun ist \alpha als Außenwinkel des Dreiecks <math>\overline{PL_1L_2}</math> so groß wie der ihm nicht anliegende Innenwinkel <math>\beta</math> dieses Dreiecks. | ||
<!--- ------------------------------------------------------------- ---> | <!--- ------------------------------------------------------------- ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Version vom 9. Mai 2013, 17:41 Uhr
ImplikationenBeispieleBeispiel 1
Beispiel 2Wenn ein Trapez ein Rechteck ist, dann sind sein Diagonalen kongruent zueinander. Beispiel 3Wenn ein Boxer während des Kampfes seinem Gegner den Rücken zukehrt, hat er den Kampf verloren. Beispiel 4Wenn zwei Winkel Stufenwinkel an geschnittenen Parallelen sind, dann sind sie kongruent zueinander. Grundlegender Aufbau
Zusammenhang zur hinreichenden BedingungIst die Aussage "Versteckte" ImplikationenBeispieleBeispiel 1: StufenwinkelsatzOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Beispiel 2: Innenwinkelsatz für DreieckeOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Beispiel 3: Umkehrung des ThalessatzesOhne Wenn-Dann
Wenn-Dann-Form
Voraussetzung
Behauptung
Implikationen als mathematische Sätzemathematische Sätze
Implikationen als Sätze
Die Implikation einer Behauptung und die Implikation als Behauptung (umgangssprachlich)
Eine gewagte Behauptung
Notwendigkeit des Beweises eines Satzes
Direkte BeweiseBeispiele für direkte BeweiseBeispiel 1: Der ScheitelwinkelsatzVorabEs sei bereits klar, dass Nebenwinkel supplementär sind (sich zu Der Satz
Der BeweisSkizzeVoraussetzung
BehauptungBeweisführung (unter Bezug auf die Beweisskizze)
q.e.d. Beispiel 2: Der starke AußenwinkelsatzVorabBereits klar sei:
Der Satz
SkizzeVoraussetzung
BehauptungBeweisDas können Sie selbst. Ergänzen Sie hier den Beweis. Orientieren Sie sich am Beweis des Scheitelwinkelsatzes. Was sind direkte Beweise?
indirekte BeweiseBespiel 1: Winkel-Seiten-Beziehung im DreieckVorab
Der Satz
VoraussetzungBehauptungAnnahme
Beweisführung
Die Annahme ist somit zu verwerfen. Beispiel 2: Eindeutigkeit des Lotes von einem Punkt auf eine GeradeKlärung der BegriffeEs seien
Der Satz
Der BeweisDie Annahme
Die Beweisführung
|

 , dann Behauptung
, dann Behauptung  .
.

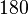 °.
°.
 und
und  Scheitelwinkel sind, so haben sie dieselbe Größe.
Scheitelwinkel sind, so haben sie dieselbe Größe.
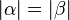
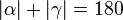 ° (Begründung:
° (Begründung:  sind Nebenwinkel und als solche supplementär.)
sind Nebenwinkel und als solche supplementär.)
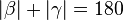 ° (Begründung:
° (Begründung: 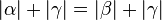 (Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.)
(Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.)
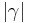 subtrahieren.)
subtrahieren.)
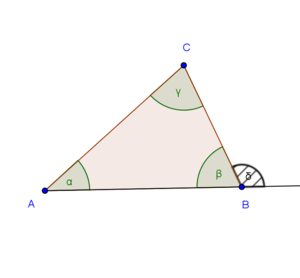
 sei ein Außenwinkel eines Dreiecks
sei ein Außenwinkel eines Dreiecks  . O.B.d.A. sei
. O.B.d.A. sei  . (Die beiden Innenwinkel, die zu
. (Die beiden Innenwinkel, die zu 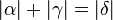
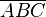 ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel
ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel 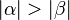
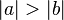
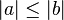 (Das Gegenteil der Behauptung)
(Das Gegenteil der Behauptung)
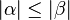 gelten muss.
gelten muss.
 eine Gerade und
eine Gerade und  ein Punkt außerhalb von
ein Punkt außerhalb von  der Lotgeraden von
der Lotgeraden von 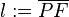
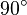 .
.
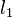 und
und 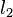 von
von 
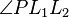
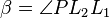 hat ebenso die Größe
hat ebenso die Größe 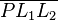 so groß wie der ihm nicht anliegende Innenwinkel
so groß wie der ihm nicht anliegende Innenwinkel 
