Implikationen
Beispiele
Beispiel 1

Wenn der BVB im Finale der Champions League das erste Tor des Spieles schießt, dann gewinnt er die Champions League der Saison 2012/13.
Beispiel 2
Wenn ein Trapez ein Rechteck ist, dann sind sein Diagonalen kongruent zueinander.
Beispiel 3
Wenn ein Boxer während des Kampfes seinem Gegner den Rücken zukehrt, hat er den Kampf verloren.
Beispiel 4
Wenn zwei Winkel Stufenwinkel an geschnittenen Parallelen sind, dann sind sie kongruent zueinander.
Grundlegender Aufbau
- Wenn Bedingung
 , dann Behauptung , dann Behauptung  . .
- Aus
 folgt folgt  . .
-

Zusammenhang zur hinreichenden Bedingung
Ist die Aussage  wahr, so ist die Bedingung der Implikation hinreichend dafür, dass die Behauptung b gilt. wahr, so ist die Bedingung der Implikation hinreichend dafür, dass die Behauptung b gilt.
"Versteckte" Implikationen
Beispiele
Beispiel 1: Stufenwinkelsatz
Ohne Wenn-Dann
- Stufenwinkel an geschnittenen Parallelen sind kongruent zueinander
Wenn-Dann-Form
- Wenn zwei Winkel Stufenwinkel an geschnittenen Parallelen sind, dann sind sie kongruent zueinander.
Voraussetzung
- die beiden Winkel sind Stufenwinkel
- an geschnittenen Parallelen
Behauptung
- die beiden Winkel sind kongruent zueinander
Beispiel 2: Innenwinkelsatz für Dreiecke
Ohne Wenn-Dann
- In jedem Dreieck beträgt die Summe der Größen seiner Innenwinkel
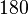 °. °.
Wenn-Dann-Form
- Wenn ein n-Eck ein Dreieck ist, dann beträgt die Summe der Größen seiner Innenwinkel
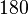 °. °.
Voraussetzung
- Das betrachtetet n-Eck ist ein Dreieck
Behauptung
- Die Summe der Größen seiner Innenwinkel beträgt
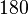 °. °.
Beispiel 3: Umkehrung des Thalessatzes
Ohne Wenn-Dann
- Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der längsten Seite dieses Dreiecks.
Wenn-Dann-Form
- Wenn ein Dreieck rechtwinklig ist, dann liegt der Mittelpunkt seines Umkreises auf der längsten seiner Seiten.
Voraussetzung
- Das betrachtete Dreieck ist rechtwinklig.
Behauptung
- Der Mittelpunkt seines Umkreises liegt auf der längsten seiner Seiten.
Implikationen als mathematische Sätze
mathematische Sätze
- Unter einem mathematischen Satz (im folgenden kurz Satz) versteht man eine mathematische Aussage, die wahr ist.
Implikationen als Sätze
- In der Regel werden Sätze als Implikationen formuliert.
- Die Voraussetzung der Implikation ist dann eine hinreichende Bedingung für die Behauptung der Implikation.
Die Implikation einer Behauptung und die Implikation als Behauptung (umgangssprachlich)
- Der Begriff der Behauptung wird natürlich auch umgangssprachlich verwendet. Meine Erfahrung lehrt mich, dass Novizen der mathematischen Logik diesbezüglich zu Verwechslungen neigen:
Eine gewagte Behauptung
- Wenn der FC Barcelona ohne Messi spielt, dann halbiert sich seine Spielstärke.
- Fans des FC Barcelona werden die gesamte Implikation (also die gesamte Aussage Wenn der FC Barcelona ohne Messi spielt, dann halbiert sich seine Spielstärke.) als eine gewagte Behauptung ansehen.
- Demgegenüber ist die Aussage Barcelona spielt ohne Messi die Voraussetzung der Implikation und die Aussage die Spielstärke halbiert sich die Behauptung der Implikation.
Notwendigkeit des Beweises eines Satzes
- Obige Implikation hinsichtlich der spielerischen Stärke des FC Barcelona in Anhängigkeit der Verfügbarkeit des Weltfußballers Messi wird nur schwer zu beweisen sein und kann damit nicht als Satz im mathematischen Sinne verstanden werden. Mathematische Sätze sind wahre Aussagen und als solche zu beweisen.
Direkte Beweise
Beispiele für direkte Beweise
Beispiel 1: Der Scheitelwinkelsatz
Vorab
Es sei bereits klar, dass Nebenwinkel supplementär sind (sich zu 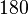 ° ergänzen). ° ergänzen).
Natürlich seien die Begriffe Scheitelwinkel und Nebenwinkel sauber definiert.
Der Satz
- Satz: (Scheitelwinkelsatz)
- Wenn zwei Winkel
 und und  Scheitelwinkel sind, so haben sie dieselbe Größe. Scheitelwinkel sind, so haben sie dieselbe Größe.
Der Beweis
Skizze
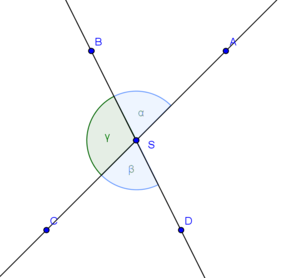
Voraussetzung
 und und  bilden ein Paar von Scheitelwinkeln bilden ein Paar von Scheitelwinkeln
Behauptung
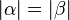
Beweisführung (unter Bezug auf die Beweisskizze)
-
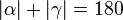 ° (Begründung: ° (Begründung:  und und  sind Nebenwinkel und als solche supplementär.) sind Nebenwinkel und als solche supplementär.)
-
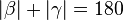 ° (Begründung: ° (Begründung:  und und  sind Nebenwinkel und als solche supplementär.) sind Nebenwinkel und als solche supplementär.)
-
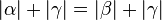 (Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.) (Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.)
-
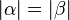 (Begründung: Auf beiden Seiten der Gleichung 3 (Begründung: Auf beiden Seiten der Gleichung 3 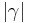 subtrahieren.) subtrahieren.)
q.e.d.
Beispiel 2: Der starke Außenwinkelsatz
Vorab
Bereits klar sei:
- Innenwinkelsumme im Dreieck beträgt
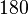 °. °.
- Nebenwinkel sind supplementär.
- Alle Begriffe sauber definiert.
Der Satz
- Satz: (starker Außenwinkelsatz)
- Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden Innenwinkel des Dreiecks, die keine Nebenwinkel dieses Außenwinkels sind.
Skizze
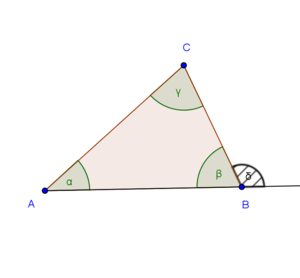
Voraussetzung
- Der Winkel
 sei ein Außenwinkel eines Dreiecks sei ein Außenwinkel eines Dreiecks  . O.B.d.A. sei . O.B.d.A. sei  Nebenwinkel vom Innenwinkel Nebenwinkel vom Innenwinkel  des Dreiecks des Dreiecks  . (Die beiden Innenwinkel, die zu . (Die beiden Innenwinkel, die zu  keine Nebenwinkel sind, seien keine Nebenwinkel sind, seien  und und  .) .)
Behauptung
Beweis
Das können Sie selbst. Ergänzen Sie hier den Beweis. Orientieren Sie sich am Beweis des Scheitelwinkelsatzes.
Was sind direkte Beweise?
- In den obigen Bespielen wurde ausgehend von der Voraussetzung und der Verwendung weiterer bereits bewiesener Sätze die Behauptung unmittelbar hergeleitet. Am Ende der Herleitungskette steht die Behauptung. Man spricht in einem solchen Fall von einem direkten Beweis.
Indirekte Beweise
Beispiel 1: Winkel-Seiten-Beziehung im Dreieck
Vorab
- Wir gehen davon aus, dass wir die Seiten-Winkel-Beziehung für Dreiecke bereits bewiesen haben: In jedem Dreieck liegt der größeren Seite auch der größere Winkel gegenüber.
Der Satz
- Satz: (Winkel-Seiten-Beziehung im Dreieck)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel  größer als der Winkel größer als der Winkel  ist, dann ist die Seite ist, dann ist die Seite  länger als die Seite länger als die Seite  . .
Voraussetzung
Behauptung
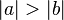
Annahme
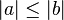 (Das Gegenteil der Behauptung) (Das Gegenteil der Behauptung)
Beweisführung
- Mittels der Annahme wird ein Widerspruch aufgedeckt
- Im speziellen Fall geht das sehr schnell:
- Aus der Annahme folgt unter Berücksichtigung der bereits bewiesenen Seiten-Winkelbeziehung, dass
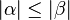 gelten muss. gelten muss.
- Letzteres ist ein Widerspruch zur Voraussetzung
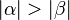 . .
Die Annahme ist somit zu verwerfen.
Beispiel 2: Eindeutigkeit des Lotes von einem Punkt auf eine Gerade
Klärung der Begriffe
Es seien  eine Gerade und eine Gerade und  ein Punkt außerhalb von ein Punkt außerhalb von  . .
- Lotgerade von
 auf auf  : Gerade, die senkrecht auf : Gerade, die senkrecht auf  steht und durch steht und durch  geht. geht.
- Lotfußpunkt des Lotes von
 auf auf  : Schnittpunkt : Schnittpunkt  der Lotgeraden von der Lotgeraden von  auf auf  mit mit  . .
- Lot l von
 auf auf  : : 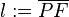
- Senkrechtstehen können sie intuitiv gebrauchen: Die Lotgerade bildet mit
 rechte Winkel, also Winkel der Größe rechte Winkel, also Winkel der Größe 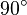 . .
Der Satz
- Wenn
 eine Gerade und eine Gerade und  ein nicht zu ein nicht zu  gehörender Punkt sind, dann gibt es höchstens ein Lot von gehörender Punkt sind, dann gibt es höchstens ein Lot von  auf auf  . .
Der Beweis
Die Annahme
- Es gibt zwei zueinander verschiedene Lote
 und und  von von  auf auf  . .
Die Beweisführung
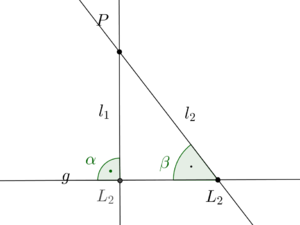
- Es sei
 der Nebenwinkel zu der Nebenwinkel zu 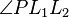
- Weil
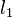 Lot von Lot von  auf auf  ist, hat ist, hat  die Größe die Größe 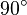 . .
- Der Winkel
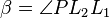 hat ebenso die Größe hat ebenso die Größe 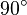 , denn auch , denn auch 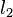 ist Lot von ist Lot von  auf auf  . .
- Nun ist
 als Außenwinkel des Dreiecks als Außenwinkel des Dreiecks 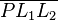 so groß wie der ihm nicht anliegende Innenwinkel so groß wie der ihm nicht anliegende Innenwinkel  dieses Dreiecks. dieses Dreiecks.
- Fehler beim Parsen(Unbekannte Funktion „\lightning“): \lightning
Letzteres ist jedoch ein Widerspruch zum Außenwinkelsatz.
- Die Annahme ist damit zu verwerfen.
Bemerkung
- In diesemBeispiel hatten wir einen Eindeutigkeitsbeweis zu führen. Wir werden solche Beweise auch Highlanderbeweise nennen (Es kann nur einen geben).
Highlanderbeweise führt man in der Regel als Widerspruchsbeweis.


Beispiel 3: Eine Gerade, die senkrecht auf dem Berührungsradius steht, ist Kreistangente
Der Satz
Präambel:
- Wir setzen zunächst ebene Geometrie voraus.
- Es seien
 ein Kreis mit dem Mittelpunkt ein Kreis mit dem Mittelpunkt  und und  eine Gerade, die mit eine Gerade, die mit  den Punkt den Punkt  gemeinsam haben möge. gemeinsam haben möge.
Implikation:
- Wenn
 senkrecht auf senkrecht auf 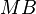 steht, dann hat steht, dann hat  mit mit  keinen weiteren von keinen weiteren von  verschiedenen Punkt gemeinsam. verschiedenen Punkt gemeinsam.
Der Beweis
Annahme

- Es existiert ein weiterer von
 verschiedener Punkt verschiedener Punkt  , den , den  und und  gemeinsam haben. gemeinsam haben.
Beweisführung
- Das können Sie selbst. Beziehen Sie sich auf die obige Skizze und verwenden Sie:
- Basiswinkelsatz
- Innenwinkelsatz
- oder Außenwinkelsatz (dann wäre die Skizze zu ergänzen).
Beweis von User Muellerm
Beweis:
1. |MB| = |MA| = Kreisradius
2. damit ist 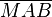 ein gleichschenkliges Dreieck ein gleichschenkliges Dreieck
3.  und und  sind Basiswinkel und haben somit die gleiche Größe sind Basiswinkel und haben somit die gleiche Größe
4. nun sind  = =  = 90° Innenwinkel des Dreiecks = 90° Innenwinkel des Dreiecks 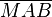 [neuer Versuch, ursprüngliche Begründung s.u.] [neuer Versuch, ursprüngliche Begründung s.u.]
5. Fehler beim Parsen(Unbekannte Funktion „\lightning“): \lightning
Widerspruch zum Innenwinkelsatz.
6. Die Annahme ist damit zu verwerfen.
[Erster, zu verwerfender, Versuch der Begründung bei 4.  = 90° (siehe Annahme), also auch = 90° (siehe Annahme), also auch  = 90°] = 90°]
--mllr 11:52, 11. Mai 2013 (CEST)
Kommentar --*m.g.* 12:54, 13. Mai 2013 (CEST)
Im ersten Versuch hatten Sie 4. mit der Annahme zu begründen versucht. Wahrscheinlich meinten Sie die Skizze, die der Annahme beigefügt wurde. Zu begründen wäre, dass  und und  jweils die Größe jweils die Größe 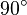 haben. Hierfür müssen zwei Begründungen geliefert werde: haben. Hierfür müssen zwei Begründungen geliefert werde:
-
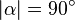 wegen der Voraussetzung (und nicht wegen der Annahme) wegen der Voraussetzung (und nicht wegen der Annahme)
-
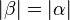 weil sie Basiswinkel sind weil sie Basiswinkel sind
Widerspruchsbeweise
Alle Beweise aus den Beispielen 1 bis 3 zu den indirekten Beweisen wurden als Widerspruchsbeweis geführt.
Der Ablauf eines Widerspruchsbeweises
Ausgangslage
- Eine Implikation
 soll bewiesen werden: soll bewiesen werden:
- Voraussetzung:
- a
- Behauptung:
- b
Formulierung der Annahme
- Wir behalten die Gültigkeit der Voraussetzung a bei und
- nehmen jedoch das Gegenteil der Behauptung an.
- Annahme:
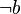
Weiterer Ablauf es Beweises
- Wir leiten aus der Annahme Schlussfolgerungen ab, die schließlich zu einem Widerspruch führen. Häufig ergibt sich dieser als Widerspruch zur Voraussetzung (Beispiel 1). Es muss sich beim Widerspruchsbeweis der Widerspruch jedoch nicht zwingend zur unmittelbar zur Voraussetzung ergeben. es können sich auch Widersprüche zu anderen Sätzen bzw. wahren Aussagen ergeben (Beispiel 2: Widerspruch zum Außenwinkelsatz).
Beweis mittels der Kontraposition einer Implikation
Begriff der Kontraposition
Beispiel 1: Kontraposition des Innenwinkelsatzes für Dreiecke
Der Innenwinkelsatz
- Wenn ein n-Eck ein Dreieck ist, dann beträgt die Summe der Größen seiner Innnenwinkel
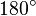
Die Voraussetzung noch einmal explizit
- Ein n-Eck
 sei ein Dreieck sei ein Dreieck
Die Behauptung noch einmal explizit
- Die Innenwinkelsumme von
 beträgt beträgt 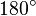 . .
Konstruktion der Kontraposition
- Bilden eine Implikation die durch Vertauschung von Voraussetzung und Behauptung der ursprünglichen Implikation entsteht. Anders ausgedrückt: Wir bilden die Umkehrung der ursprünglichen Implikation: Wenn in einem n-Eck
 die Innenwinkelsumme die Innenwinkelsumme 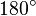 beträgt, dann ist beträgt, dann ist  ein Dreieck. ein Dreieck.
- Wir negieren in der Umkehrung die Voraussetzung und die Behauptung: Wenn in einem n-Eck
 die Innenwinkelsumme verschieden von die Innenwinkelsumme verschieden von 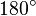 ist, dann ist ist, dann ist  kein Dreieck. kein Dreieck.
Definition des Begriffs der Kontraposition
Definition
(Kontraposition einer Implikation)
Unter der Kontraposition der Implikation  versteht man die Implikation versteht man die Implikation 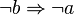 . .
Bedeutung der Kontraposition einer Implikation für das Beweisen dieser Implikation
Eine Übung
Satz des Pythagoras
- Wenn ein Dreieck rechtwinklig ist, dann ist die Summe der Quadrate der Längen der Katheten gleich dem Quadrat der Länge der Hypotenuse.
- Wahrheitswert des Satzes von Pythagoras:
- Umkehrung des Satzes von Pythagoras:
- Wahrheitswert der Umkehrung des Satzes von Pythagoras:
- Kontraposition des Satzes von Pythagoras:
- Wahrheitswert der Kontraposition:
Eigenschaften von Quadratdiagonalen
- Implikation 1: Wenn ein Viereck ein Quadrat ist, dann halbieren sich seine Diagonalen.
- Wahrheitswert von Implikation 1:
- Umkehrung von Implikation 1:
- Wahrheitswert der Umkehrung von Implikation 1:
- Kontraposition von Implikation 1:
- Wahrheitswert der Kontraposition von Implikation 1:
Nebenwinkelsatz
- Nebenwinkelsatz:
- Wahrheitswert des Nebenwinkelsatzes:
- Umkehrung des Nebenwinkelsatzes:
- Wahrheitswert der Umkehrung des Nebenwinkelsatzes:
- Kontraposition des Nebenwinkelsatzes:
- Wahrheitswert der Kontraposition des Nebenwinkelsatzes:
Scheitelwinkelsatz
- Scheitelwinkelsatz:
- Wahrheitswert des Scheitelwinkelsatzes:
- Umkehrung des Scheitelwinkelsatzes:
- Wahrheitswert der Umkehrung des Scheitelwinkelsatzes:
- Kontraposition des Scheitelwinkelsatzes:
- Wahrheitswert der Kontraposition des Scheitelwinkelsatzes:
|

 , dann Behauptung
, dann Behauptung  .
.

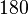 °.
°.
 und
und  Scheitelwinkel sind, so haben sie dieselbe Größe.
Scheitelwinkel sind, so haben sie dieselbe Größe.

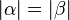
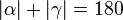 ° (Begründung:
° (Begründung:  sind Nebenwinkel und als solche supplementär.)
sind Nebenwinkel und als solche supplementär.)
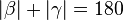 ° (Begründung:
° (Begründung: 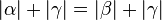 (Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.)
(Begründung: linke Seite von Gleichung 1 ist gleich der linken Seite von Geleichung 2.)
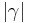 subtrahieren.)
subtrahieren.)

 sei ein Außenwinkel eines Dreiecks
sei ein Außenwinkel eines Dreiecks  . O.B.d.A. sei
. O.B.d.A. sei  . (Die beiden Innenwinkel, die zu
. (Die beiden Innenwinkel, die zu 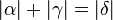
 ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel
ein Dreieck mit den schulüblichen Bezeichnungen. Wenn der Winkel 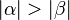
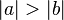
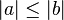 (Das Gegenteil der Behauptung)
(Das Gegenteil der Behauptung)
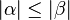 gelten muss.
gelten muss.
 eine Gerade und
eine Gerade und  ein Punkt außerhalb von
ein Punkt außerhalb von  der Lotgeraden von
der Lotgeraden von 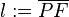
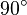 .
.
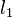 und
und 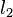 von
von 
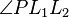
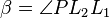 hat ebenso die Größe
hat ebenso die Größe 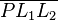 so groß wie der ihm nicht anliegende Innenwinkel
so groß wie der ihm nicht anliegende Innenwinkel 

 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  und
und  gemeinsam haben möge.
gemeinsam haben möge.
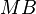 steht, dann hat
steht, dann hat 
 , den
, den 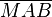 ein gleichschenkliges Dreieck
ein gleichschenkliges Dreieck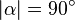 wegen der Voraussetzung (und nicht wegen der Annahme)
wegen der Voraussetzung (und nicht wegen der Annahme)
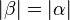 weil sie Basiswinkel sind
weil sie Basiswinkel sind
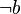
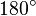
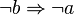 .
.

