Definition der Woche 3 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Definition von Blueberry) |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
Definieren Sie den Begriff der Parabel als Menge von Punkte, die gewisse Abstandseigenschaften bezüglich <math>F</math> und <math>l</math> haben. | Definieren Sie den Begriff der Parabel als Menge von Punkte, die gewisse Abstandseigenschaften bezüglich <math>F</math> und <math>l</math> haben. | ||
| + | ==Mögliche Definition:== | ||
| + | ===Definition von Blueberry=== | ||
| + | Es seien l eine Gerade und F ein Punkt außerhalb von l. Zudem liegt auf l ein Punkt L. <br /> | ||
| + | Die Menge aller Punkte, die von dem Schnittpunkt P der Mittelsenkrechten von der Strecke LF mit der Senkrechten auf l in L den gleichen Abstand haben, nennt man Parabel mit dem Brennpunkt F und der Leitgeraden l.--[[Benutzer:Blueberry|Blueberry]] 18:24, 17. Mai 2013 (CEST) | ||
| + | ====Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 19:02, 21. Mai 2013 (CEST)==== | ||
| + | Der Punkt P ist ja gerade ein Punkt der Parabel. So wie Sie formulieren bekommen wir keine Parabel. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
</div> | </div> | ||
| − | [[Category:Einführung_S]] | + | [[Category:Einführung_S]]<br /><br /><br /> |
Aktuelle Version vom 21. Mai 2013, 19:03 Uhr
Es seien 
eine Gerade und 
ein Punkt außerhalb von . Auf sei ein Punkt 
gegeben. Der Schnittpunkt 
der Mittelsenkrechten von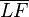 
mit der Senkrechten auf in ist ein Punkt der Parabel mit dem Brennpunkt und der Leitgeraden .
Definieren Sie den Begriff der Parabel als Menge von Punkte, die gewisse Abstandseigenschaften bezüglich und haben.
Mögliche Definition:
Definition von Blueberry
Es seien l eine Gerade und F ein Punkt außerhalb von l. Zudem liegt auf l ein Punkt L.
Die Menge aller Punkte, die von dem Schnittpunkt P der Mittelsenkrechten von der Strecke LF mit der Senkrechten auf l in L den gleichen Abstand haben, nennt man Parabel mit dem Brennpunkt F und der Leitgeraden l.--Blueberry 18:24, 17. Mai 2013 (CEST)
Bemerkung --*m.g.* 19:02, 21. Mai 2013 (CEST)
Der Punkt P ist ja gerade ein Punkt der Parabel. So wie Sie formulieren bekommen wir keine Parabel.
