Lösung von Aufgabe 11.09 SoSe 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Gegeben seien der Winkel <math>\alpha = \angle ASB</math>, die Winkelhalbierende w von <math>\alpha</math> und der Punkt P mit <math>\overline{PA} \tilde {=} \ov…“)
 
Zeile 32: Zeile 32:
  
 
--[[Benutzer:Illu13|Illu13]] 23:02, 10. Jul. 2013 (CEST)
 
--[[Benutzer:Illu13|Illu13]] 23:02, 10. Jul. 2013 (CEST)
 +
 +
[[Kategorie: Einführung_S]]

Version vom 10. Juli 2013, 22:05 Uhr

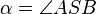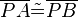
Gegeben seien der Winkel \alpha = \angle ASB, die Winkelhalbierende w von \alpha und der Punkt P mit \overline{PA} \tilde {=} \overline{PB}

z.z.: P \in w

Beweis:

1) 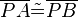\overline{PA} \tilde {=} \overline{PB} ; (>Voraussetzung)

2) 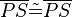\overline{PS} \tilde {=} \overline{PS} ; (>trivial)

3) Sei m die Mittelsenkrechte von \overline{AB} und M der Mittelpunkt von \overline{AB} ; (>Existenz der Mittelsenkrechten)

4) 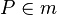P\in m ; (>Def. Mittelsenkrechte, (1))

5) 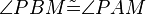\angle PBM \tilde {=} \angle PAM ; (>(1),Basiswinkelsatz)

6) 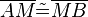\overline{AM} \tilde {=} \overline{MB} ; (>(3))

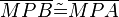7) \overline{MPB} \tilde {=} \overline{MPA} ; (>(1),(5),(6),sws)

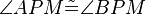8) \angle APM \tilde {=} \angle BPM; (>(7))

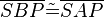9) \overline{SBP} \tilde {=} \overline{SAP} ; (>(1),(8),(2),sws)

10) 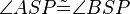\angle ASP \tilde {=} \angle BSP; (>(9))

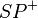11) \ SP^{+} ist die Winkelhalbierende w; (>(10), Def. und Eindeutigkeit der Winkelhalbierenden)

12) 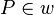P\in w; (>(11))

Muss ich hier explizit sagen, dass P im Inneren vom Winkel liegt? Darf ich das voraussetzen oder muss ich eine Fallunterscheidung machen?

--Illu13 23:02, 10. Jul. 2013 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_11.09_SoSe_13&oldid=24426“