Wir waren auf den Königsstuhl SoSe 2013: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Beweisen wie die Schüler) |
*m.g.* (Diskussion | Beiträge) (→Beweisen wie die Schüler) |
||
| Zeile 32: | Zeile 32: | ||
====Beweisen wie die Schüler==== | ====Beweisen wie die Schüler==== | ||
Die Anzahl der Punkte, die es für jeden Schritt des Beweises gibt, ist gleichzeitig ein Hinweis auf die Mächtigkeit der Menge der Begründungen. Eine eventuelle Begründung ''mit Rechnen in <math>\mathbb{R}</math>'' ist dabei nicht berücksichtigt. | Die Anzahl der Punkte, die es für jeden Schritt des Beweises gibt, ist gleichzeitig ein Hinweis auf die Mächtigkeit der Menge der Begründungen. Eine eventuelle Begründung ''mit Rechnen in <math>\mathbb{R}</math>'' ist dabei nicht berücksichtigt. | ||
| + | ====Wie tief gehen die Begründungen==== | ||
| + | Bei Aufgaben, die die Kongruenzgeometrie voraussetzen, braucht nicht mehr mit den Inzidenzaxiomen begründet werden. Wir gehen davon aus, dass jede Gerade unendlich viele Punte hat. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
<!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
|} | |} | ||




 geschafft
geschafft 



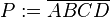 ein weißes Blatt Papier im Format DIN A4. Wie faltet man mit
ein weißes Blatt Papier im Format DIN A4. Wie faltet man mit  ein Parallelogramm, wenn man die Seiten
ein Parallelogramm, wenn man die Seiten 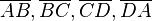 in keiner Art und Weise für die Faltkonstruktion verwenden darf?
in keiner Art und Weise für die Faltkonstruktion verwenden darf?
 ist dabei nicht berücksichtigt.
ist dabei nicht berücksichtigt.

