Lösung von Aufg. 12.05 SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Lösung) |
*m.g.* (Diskussion | Beiträge) (→Lösung) |
||
| Zeile 8: | Zeile 8: | ||
==Lösung== | ==Lösung== | ||
| − | Es sei <math>\overline{ABC}</math> ein Dreieck. Wenn <math>AB</math>, <math>BC</math> und <math>AC</math> Tangenten ein und desselben Kreises <math>k</math> sind, dann ist <math>k</math> | + | Es sei <math>\overline{ABC}</math> ein Dreieck. Wenn <math>AB</math>, <math>BC</math> und <math>AC</math> Tangenten ein und desselben Kreises <math>k</math> sind, dann ist <math>k</math> Inkreis von <math>\overline{ABC}</math>.--[[Benutzer:*m.g.*|*m.g.*]] 22:38, 18. Jul. 2013 (CEST)<br /> |
Zurück zu: [[Serie 12 SoSe 2013]] | Zurück zu: [[Serie 12 SoSe 2013]] | ||
Aktuelle Version vom 18. Juli 2013, 22:38 Uhr
Aufgabe 12.05Definieren Sie den Begriff Inkreis eines Dreiecks unter der Verwendung des Begriffs Tangente.
LösungEs sei Zurück zu: Serie 12 SoSe 2013 |
ein Dreieck. Wenn 
, 
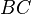und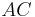 
Tangenten ein und desselben Kreises 
sind, dann ist 
