Lösung von Aufg. 11.03 SoSe 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="background…“)
 
Zeile 3: Zeile 3:
 
| valign="top" |
 
| valign="top" |
  
−
 
+
==Aufgabe 11.03 ==
 +
Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt auf eine Gerade.<br />
  
  
 
==Lösung==
 
==Lösung==
 +
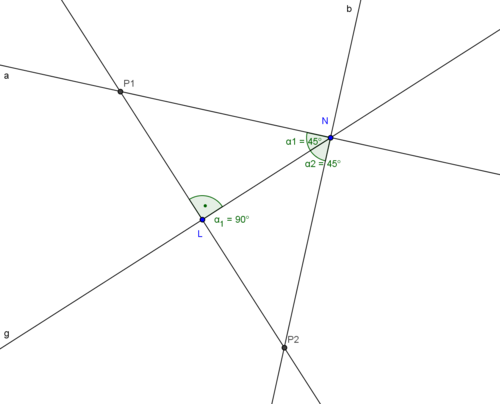
===Existenz===
 +
[[Bild:Lot.png|500px]]
 +
 +
{| class="wikitable center"
 +
|+ EXISTENZ
 +
|- style="background: #DDFFDD;"
 +
!
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
! style="background: #FFDDDD;"|(I)
 +
| Konstruiere einen Punkt N auf g.<br />Fall 1: Falls <math>P1N \perp g</math>, dann ist <math>\overline{P1N}</math> unser Lot.<br />Fall 2: <math>P1N \not\perp g</math>, dann weiter mit (II)
 +
| Konstruktion, (Gerade ist Menge von Punkten)
 +
|-
 +
! style="background: #FFDDDD;"|(II)
 +
| Antragen von <math>\alpha1: \alpha1 \cong \alpha2</math>
 +
| Konstruktion, Winkelkonstruktionsaxiom
 +
|-
 +
! style="background: #FFDDDD;"|(III)
 +
| Antragen von <math>|NP|1: |NP1| \cong\ |NP2|</math>
 +
| Konstruktion, Axiom vom Lineal
 +
|-
 +
! style="background: #FFDDDD;"|(IV)
 +
| Antragen von <math>|NL| \cong\ |NL|</math>
 +
| trivial
 +
|-
 +
! style="background: #FFDDDD;"|(V)
 +
| <math>\overline{LNP1} \cong\ \overline{LNP2}</math>
 +
| (II), (III), (IV), SWS
 +
|-
 +
! style="background: #FFDDDD;"|(VI)
 +
| <math>\angle NLP1 \cong\ \angle NLP2</math>
 +
| beides rechte Winkel  --> <math>\overline{PN}</math> ist Lot auf g.
 +
|}
 +
 +
 +
[[Bild:Lot2.png|500px]]
  
 
Zurück zu: [[Serie 11 SoSe 2013]]
 
Zurück zu: [[Serie 11 SoSe 2013]]

Version vom 18. Juli 2013, 23:41 Uhr

Aufgabe 11.03

Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt auf eine Gerade.


Lösung

Existenz

Lot.png

EXISTENZ
Beweisschritt Begründung
(I) Konstruiere einen Punkt N auf g.
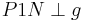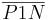Fall 1: Falls P1N \perp g, dann ist \overline{P1N} unser Lot.
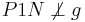Fall 2: P1N \not\perp g, dann weiter mit (II) 		Konstruktion, (Gerade ist Menge von Punkten)
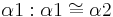
(II) Antragen von \alpha1: \alpha1 \cong \alpha2 Konstruktion, Winkelkonstruktionsaxiom
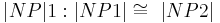
(III) Antragen von |NP|1: |NP1| \cong\ |NP2| Konstruktion, Axiom vom Lineal
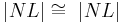
(IV) Antragen von |NL| \cong\ |NL| trivial
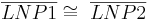
(V) \overline{LNP1} \cong\ \overline{LNP2} (II), (III), (IV), SWS
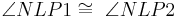
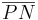(VI) \angle NLP1 \cong\ \angle NLP2 beides rechte Winkel --> \overline{PN} ist Lot auf g.


Lot2.png

Zurück zu: Serie 11 SoSe 2013

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._11.03_SoSe_13&oldid=24945“