Lösung von Aufg. 11.03 SoSe 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Eindeutigkeit)
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 23: Zeile 23:
 
|-
 
|-
 
! style="background: #FFDDDD;"|(II)
 
! style="background: #FFDDDD;"|(II)
−
| Antragen von <math>\alpha1: \alpha1 \cong \alpha2</math>
+
| Antragen von <math>\alpha1: \alpha1 \tilde= \alpha2</math>
 
| Konstruktion, Winkelkonstruktionsaxiom
 
| Konstruktion, Winkelkonstruktionsaxiom
 
|-
 
|-
 
! style="background: #FFDDDD;"|(III)
 
! style="background: #FFDDDD;"|(III)
−
| Antragen von <math>|NP|1: |NP1| \cong\ |NP2|</math>
+
| Antragen von <math>|NP|1: |NP1| \tilde=\ |NP2|</math>
 
| Konstruktion, Axiom vom Lineal
 
| Konstruktion, Axiom vom Lineal
 
|-
 
|-
 
! style="background: #FFDDDD;"|(IV)
 
! style="background: #FFDDDD;"|(IV)
−
| Antragen von <math>|NL| \cong\ |NL|</math>
+
| Antragen von <math>|NL| \tilde=\ |NL|</math>
 
| trivial
 
| trivial
 
|-
 
|-
 
! style="background: #FFDDDD;"|(V)
 
! style="background: #FFDDDD;"|(V)
−
| <math>\overline{LNP1} \cong\ \overline{LNP2}</math>
+
| <math>\overline{LNP1} \tilde=\ \overline{LNP2}</math>
 
| (II), (III), (IV), SWS
 
| (II), (III), (IV), SWS
 
|-
 
|-
 
! style="background: #FFDDDD;"|(VI)
 
! style="background: #FFDDDD;"|(VI)
−
| <math>\angle NLP1 \cong\ \angle NLP2</math>
+
| <math>\angle NLP1 \tilde=\ \angle NLP2</math>
 
| beides rechte Winkel  --> <math>\overline{PN}</math> ist Lot auf g.
 
| beides rechte Winkel  --> <math>\overline{PN}</math> ist Lot auf g.
 
|}
 
|}
  
  
−
[[Bild:Lot2.png|500px]]
+
Dieser Beweis wurde im SoSe 2010 von Studierenden selbständig im Wiki erbracht. --[[Benutzer:*m.g.*|*m.g.*]] 23:44, 18. Jul. 2013 (CEST)
−
 
+
===Eindeutigkeit===
 +
Es sei <math>\overline{PL}</math> das Lot von <math>P</math> auf <math>g</math>. Annahme: <math>\overline{PA}</math> mit <math>A \not = L</math> ist auch Lot von <math>P</math> auf <math>g</math>. Dann hätte das Dreieck <math>\overline{PLA}</math> zwei rechte Innenwinkel, was ein Widerspruch zu den Folgerungen aus dem schwachen Außenwinkelsatz ist.<br /><br />--[[Benutzer:*m.g.*|*m.g.*]] 23:48, 18. Jul. 2013 (CEST)<br />
 
Zurück zu: [[Serie 11 SoSe 2013]]
 
Zurück zu: [[Serie 11 SoSe 2013]]
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
<!--- Was hier drunter steht muss stehen bleiben --->

Aktuelle Version vom 18. Juli 2013, 23:48 Uhr

Inhaltsverzeichnis

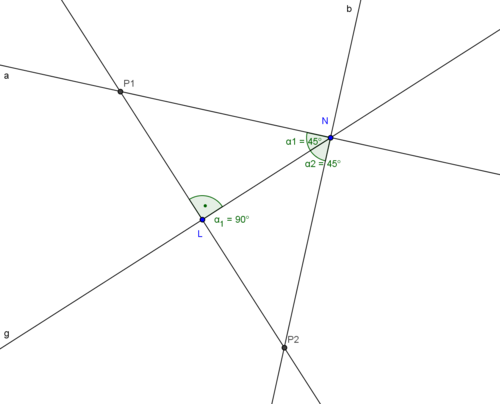
Aufgabe 11.03

Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt auf eine Gerade.


Lösung

Existenz

Lot.png

EXISTENZ
Beweisschritt Begründung
(I) Konstruiere einen Punkt N auf g.
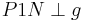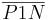Fall 1: Falls P1N \perp g, dann ist \overline{P1N} unser Lot.
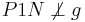Fall 2: P1N \not\perp g, dann weiter mit (II) 		Konstruktion, (Gerade ist Menge von Punkten)
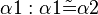
(II) Antragen von \alpha1: \alpha1 \tilde= \alpha2 Konstruktion, Winkelkonstruktionsaxiom
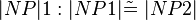
(III) Antragen von |NP|1: |NP1| \tilde=\ |NP2| Konstruktion, Axiom vom Lineal
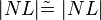
(IV) Antragen von |NL| \tilde=\ |NL| trivial
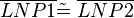
(V) \overline{LNP1} \tilde=\ \overline{LNP2} (II), (III), (IV), SWS
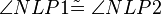
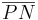(VI) \angle NLP1 \tilde=\ \angle NLP2 beides rechte Winkel --> \overline{PN} ist Lot auf g.


Dieser Beweis wurde im SoSe 2010 von Studierenden selbständig im Wiki erbracht. --*m.g.* 23:44, 18. Jul. 2013 (CEST)

Eindeutigkeit

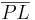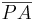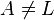Es sei \overline{PL} das Lot von P auf g. Annahme: \overline{PA} mit A \not = L ist auch Lot von 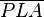P auf g. Dann hätte das Dreieck \overline{PLA} zwei rechte Innenwinkel, was ein Widerspruch zu den Folgerungen aus dem schwachen Außenwinkelsatz ist.

--*m.g.* 23:48, 18. Jul. 2013 (CEST)
Zurück zu: Serie 11 SoSe 2013

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._11.03_SoSe_13&oldid=24952“