Übung 3: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgabe 1= Entwickeln Sie eine Parameterdarstellung für Kreisevolventen. =Aufgabe 2= Ein Punkt <math>P</math> bewege sich auf einem Kreis mit konstanter Winkelg…“) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Ein Punkt <math>P</math> bewege sich auf einem Kreis mit konstanter Winkelgeschwindigkeit. Für eine Umdrehung benötige er die Zeit <math>T</math>. Beschreiben Sie die Bewegung von <math>P</math> in Anhängigkeit von der Zeit <math>t</math>. | Ein Punkt <math>P</math> bewege sich auf einem Kreis mit konstanter Winkelgeschwindigkeit. Für eine Umdrehung benötige er die Zeit <math>T</math>. Beschreiben Sie die Bewegung von <math>P</math> in Anhängigkeit von der Zeit <math>t</math>. | ||
=Aufgabe 3= | =Aufgabe 3= | ||
| − | Informieren Sie sich über den Begriff archimedische Spirale und generieren Sie archimedische Spiralen mittels Geogebra und mittels Excel. | + | Informieren Sie sich über den Begriff archimedische Spirale und generieren Sie archimedische Spiralen mittels Geogebra und mittels Excel.. |
| + | |||
| + | [[Kategorie:Linalg]] | ||
Aktuelle Version vom 2. Dezember 2013, 11:56 Uhr
Aufgabe 1
Entwickeln Sie eine Parameterdarstellung für Kreisevolventen.
Aufgabe 2
Ein Punkt 
bewege sich auf einem Kreis mit konstanter Winkelgeschwindigkeit. Für eine Umdrehung benötige er die Zeit 
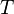. Beschreiben Sie die Bewegung von in Anhängigkeit von der Zeit 
.
Aufgabe 3
Informieren Sie sich über den Begriff archimedische Spirale und generieren Sie archimedische Spiralen mittels Geogebra und mittels Excel..
